题目内容
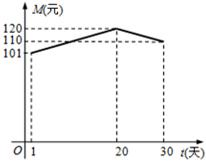 经市场调查分析,某旅游城市在上月内(以30天计算),第t天旅游人数S(万人)与时间t满足:S-4与t成反比,且上月第20天旅游人数为4.05万人,又第t天旅游人均消费M(元)与时间t的关系如图所示.
经市场调查分析,某旅游城市在上月内(以30天计算),第t天旅游人数S(万人)与时间t满足:S-4与t成反比,且上月第20天旅游人数为4.05万人,又第t天旅游人均消费M(元)与时间t的关系如图所示.(I)求该城市上月的旅游日收益y(万元)与时间t(1≤t≤30,t∈N)的函数关系式;
(II)求y的最小值;
(Ⅲ)问该城市上月内哪几天旅游日收益不低于481万元?
(注:旅游日收益=日旅游人数×日旅游人均消费)
分析:(I)由题意可设S-4=
,将t=20,S=4.05代入,求出k,根据图象求出M,从而根据旅游日收益=日旅游人数×日旅游人均消费求出旅游日收益;
(II)当1≤t≤20,t∈N时利用基本不等式进行求最值,当21≤t≤30,t∈N时,利用导数研究函数的最值即可;
(III)根据分段函数的意义可在每一段上建立不等式,解出符合条件的t,问题即可得解.
| k |
| t |
(II)当1≤t≤20,t∈N时利用基本不等式进行求最值,当21≤t≤30,t∈N时,利用导数研究函数的最值即可;
(III)根据分段函数的意义可在每一段上建立不等式,解出符合条件的t,问题即可得解.
解答:解:(I)由题意可设S-4=
,
将t=20,S=4.05代入,得k=1,所以S=
+4.(2分)
由图象可得M=
(4分)
所以旅游日收益y=
=
(II)当1≤t≤20,t∈N时,y=
+4t+401≥2
+401=441
当且仅当
=4t,即t=5时取到等号.(8分)
当21≤t≤30,t∈N时,因为y′=-
-4<0,
所以y=
-4t+559在21≤t≤30,t∈N是单调递减,
所以当t=30时,ymin=443
.(10分)
综上可知,上月在第5天旅游日收益的最小值为441元.(11分)
(Ⅲ)当1≤t≤20,t∈N时,由
+4t+401≥481,得t2-20t+25≥0,
解得t≥10+5
或t≤10-5
,所以t=19,20,1.(13分)
当21≤t≤30,t∈N时,由
-4t+559≥481,得2t2-39t-70≤0,
解得
≤t≤
,所以t=21.(15分)
综上可知,该城市上月第1、19、20、21四个旅游日收益不低于481万元.(16分)
| k |
| t |
将t=20,S=4.05代入,得k=1,所以S=
| 1 |
| t |
由图象可得M=
|
所以旅游日收益y=
|
|
(II)当1≤t≤20,t∈N时,y=
| 100 |
| t |
|
当且仅当
| 100 |
| t |
当21≤t≤30,t∈N时,因为y′=-
| 140 |
| t2 |
所以y=
| 140 |
| t |
所以当t=30时,ymin=443
| 2 |
| 3 |
综上可知,上月在第5天旅游日收益的最小值为441元.(11分)
(Ⅲ)当1≤t≤20,t∈N时,由
| 100 |
| t |
解得t≥10+5
| 3 |
| 3 |
当21≤t≤30,t∈N时,由
| 140 |
| t |
解得
39-4
| ||
| 4 |
39+4
| ||
| 4 |
综上可知,该城市上月第1、19、20、21四个旅游日收益不低于481万元.(16分)
点评:本题主要考查学生根据实际情况选择函数类型的能力,以及基本不等式在求函数最值中的应用能力.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
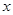 万件,需另投入流动成本为
万件,需另投入流动成本为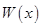 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,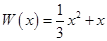 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,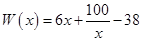 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完. (万元)关于年产量
(万元)关于年产量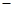 固定成本
固定成本 万件,需另投入流动成本为
万件,需另投入流动成本为 万元,在年产量不足8万件时,
万元,在年产量不足8万件时,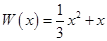 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,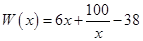 (万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元). 通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.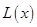 (万元)关于年产量
(万元)关于年产量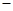 固定成本
固定成本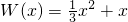 (万元),在年产量不小于8万件时,
(万元),在年产量不小于8万件时,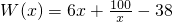 (万元).通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.
(万元).通过市场分析,每件产品售价为5元时,生产的商品能当年全部售完.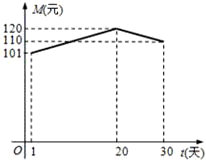 经市场调查分析,某旅游城市在上月内(以30天计算),第t天旅游人数S(万人)与时间t满足:S-4与t成反比,且上月第20天旅游人数为4.05万人,又第t天旅游人均消费M(元)与时间t的关系如图所示.
经市场调查分析,某旅游城市在上月内(以30天计算),第t天旅游人数S(万人)与时间t满足:S-4与t成反比,且上月第20天旅游人数为4.05万人,又第t天旅游人均消费M(元)与时间t的关系如图所示.