题目内容
9.已知两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0,分别求满足下列条件的a,b值(1)l1⊥l2,且直线l1过点(-3,-1);
(2)l1∥l2,且直线l1在两坐标轴上的截距相等.
分析 (1)由直线垂直和直线l1过定点可得ab的方程组,解方程组可得;
(2)由直线平行和直线l1截距相等可得ab的方程组,解方程组可得.
解答 解:(1)∵两直线l1:ax-by+4=0,l2:(a-1)x+y+b=0且l1⊥l2,
∴a(a-1)+(-b)×1=0,即a2-a-b=0,
又∵直线l1过点(-3,-1),∴-3a+b+4=0,
联立解得a=2,b=2;
(2)由l1∥l2可得a×1-(-b)(a-1)=0,即a+ab-b=0,
在方程ax-by+4=0中令x=0可得y=$\frac{4}{b}$,令y=0可得x=-$\frac{4}{a}$,
∴$\frac{4}{b}$=-$\frac{4}{a}$,即b=-a,联立解得a=2,b=-2.
点评 本题考查直线的一般式方程和平行垂直关系,涉及直线的截距,属基础题.

练习册系列答案
相关题目
19.下列各组函数中,表示同一函数的是( )
| A. | y=1,y=x0 | B. | y=lgx2,y=2lgx | C. | $y=|x|,y={(\sqrt{x})^2}$ | D. | $y=x,y=\root{3}{x^3}$ |
20.函数y=log2|x|的图象特点为( )
| A. | 关于x轴对称 | B. | 关于y轴对称 | C. | 关于原点对称 | D. | 关于直线y=x对称 |
17.在西非肆虐的“埃博拉病毒”的传播速度很快,这已经成为全球性的威胁.为了考察某种埃博拉病毒疫苗的效果,现随机抽取100只小鼠进行试验,得到如下列联表:
附表:
参照附表,下列结论正确的是( )
| 感染 | 未感染 | 总计 | |
| 服用 | 10 | 40 | 50 |
| 未服用 | 20 | 30 | 50 |
| 总计 | 30 | 70 | 100 |
| P(K2≥k) | 0.10 | 0.05 | 0.025 |
| k | 2.76 | 3.841 | 5.024 |
| A. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗有关” | |
| B. | 在犯错误的概率不超5%过的前提下,认为“小动物是否被感染与有没有服用疫苗无关” | |
| C. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗有关” | |
| D. | 有97.5%的把握认为“小动物是否被感染与有没有服用疫苗无关” |
19.下列命题中不正确的是( )
| A. | logab•logbc•logca=1(a,b,c均为不等于1的正数) | |
| B. | 若xlog34=1,则${4^x}+{4^{-x}}=\frac{10}{3}$ | |
| C. | 函数f(x)=lnx满足f(a+b)=f(a)•f(b)(a,b>0) | |
| D. | 函数f(x)=lnx满足f(a•b)=f(a)+f(b)(a,b>0) |
 已知函数f(x)=$\left\{\begin{array}{l}{|4-{x}^{2}|,x≤0}\\{{2}^{2-x},0<x≤2}\\{lo{g}_{2}x,x>2}\end{array}\right.$,
已知函数f(x)=$\left\{\begin{array}{l}{|4-{x}^{2}|,x≤0}\\{{2}^{2-x},0<x≤2}\\{lo{g}_{2}x,x>2}\end{array}\right.$,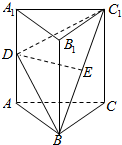 如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.
如图,在三棱柱ABC-A1B1C1中,△ABC为等边三角形,侧棱AA1⊥平面ABC,AB=2,AA1=2$\sqrt{3}$,D、E分别为AA1、BC1的中点.