题目内容
已知△ABC的面积满足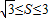 ,且
,且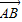 •
•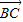 =6,
=6,(Ⅰ)求f(B)=sin2B+2sinB•cosB+3cos2B的值域;
(Ⅱ)若
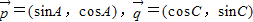 ,求
,求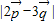 的取值范围.
的取值范围.
【答案】分析:(I)由三角形面积和数量积公式,联解可得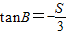 ,结合
,结合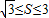 得tanB∈[-1,-
得tanB∈[-1,-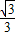 ],从而
],从而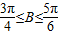 ,再化简函数f(B)=2+
,再化简函数f(B)=2+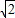 sin(2B+
sin(2B+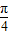 ),结合三角函数的图象与性质,可得函数f(B)的值域;
),结合三角函数的图象与性质,可得函数f(B)的值域;
(II)由已知得向量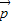 、
、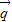 都是单位向量,将
都是单位向量,将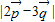 平方化简得
平方化简得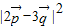 =13-12sinB,结合角B的取值范围则不难得到
=13-12sinB,结合角B的取值范围则不难得到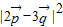 的取值范围,进而可得到
的取值范围,进而可得到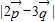 的取值范围.
的取值范围.
解答:解(I)由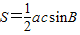 ,得2S=acsinB
,得2S=acsinB
因为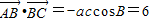 ,所以-6=accosB
,所以-6=accosB
∴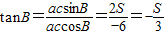 ,
,
结合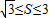 ,得
,得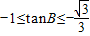 ,
,
由角B为三角形内角可知,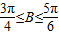 …(2分).
…(2分).
∵f(B)=sin2B+2sinB•cosB+3cos2B=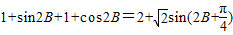 …(4分)
…(4分)
∵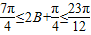 ,函数f(B)在区间[
,函数f(B)在区间[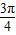 ,
,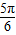 ]上为增函数
]上为增函数
∴当B=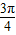 时,函数有最小值为2+
时,函数有最小值为2+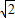 sin
sin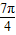 =1;当B=
=1;当B=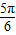 时,函数有最大值为2+
时,函数有最大值为2+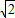 sin
sin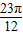 =
=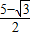
由此可得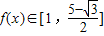 …(6分).
…(6分).
(II)由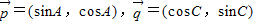 可知:
可知: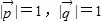 .…(8分).
.…(8分).
∵A+B+C=π,∴A+C=π-B,得sin(A+C)=sinB
因此,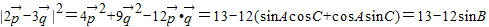 …(10分)
…(10分)
∵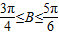 ,∴sinB∈[
,∴sinB∈[ ,
,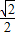 ]
]
由此可得: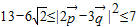 ,得到
,得到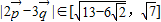 …(12分).
…(12分).
点评:本题以平面向量的数量积运算为载体,求关于B的函数的值域和向量模长的取值范围,着重考查了平面向量数量积的运算公式、两角和与差的正弦函数和向量的模公式等知识,属于中档题.
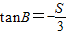 ,结合
,结合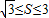 得tanB∈[-1,-
得tanB∈[-1,-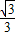 ],从而
],从而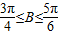 ,再化简函数f(B)=2+
,再化简函数f(B)=2+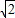 sin(2B+
sin(2B+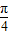 ),结合三角函数的图象与性质,可得函数f(B)的值域;
),结合三角函数的图象与性质,可得函数f(B)的值域;(II)由已知得向量
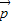 、
、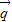 都是单位向量,将
都是单位向量,将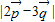 平方化简得
平方化简得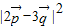 =13-12sinB,结合角B的取值范围则不难得到
=13-12sinB,结合角B的取值范围则不难得到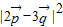 的取值范围,进而可得到
的取值范围,进而可得到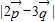 的取值范围.
的取值范围.解答:解(I)由
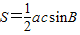 ,得2S=acsinB
,得2S=acsinB因为
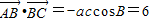 ,所以-6=accosB
,所以-6=accosB∴
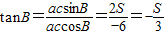 ,
,结合
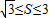 ,得
,得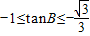 ,
,由角B为三角形内角可知,
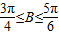 …(2分).
…(2分).∵f(B)=sin2B+2sinB•cosB+3cos2B=
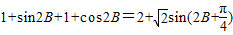 …(4分)
…(4分)∵
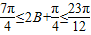 ,函数f(B)在区间[
,函数f(B)在区间[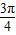 ,
,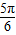 ]上为增函数
]上为增函数∴当B=
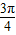 时,函数有最小值为2+
时,函数有最小值为2+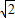 sin
sin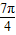 =1;当B=
=1;当B=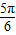 时,函数有最大值为2+
时,函数有最大值为2+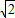 sin
sin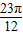 =
=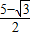
由此可得
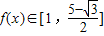 …(6分).
…(6分).(II)由
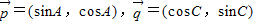 可知:
可知: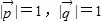 .…(8分).
.…(8分).∵A+B+C=π,∴A+C=π-B,得sin(A+C)=sinB
因此,
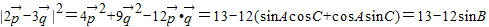 …(10分)
…(10分)∵
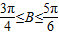 ,∴sinB∈[
,∴sinB∈[ ,
,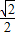 ]
]由此可得:
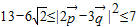 ,得到
,得到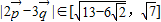 …(12分).
…(12分).点评:本题以平面向量的数量积运算为载体,求关于B的函数的值域和向量模长的取值范围,着重考查了平面向量数量积的运算公式、两角和与差的正弦函数和向量的模公式等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
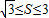 ,且
,且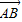 •
•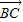 =6,
=6,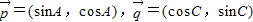 ,求
,求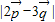 的取值范围.
的取值范围.