题目内容
已知向量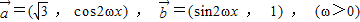 ,令
,令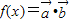 ,且f(x)的周期为π.
,且f(x)的周期为π.(Ⅰ)求函数f(x)的解析式;
(Ⅱ)若
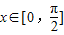 时f(x)+m≤3,求实数m的取值范围.
时f(x)+m≤3,求实数m的取值范围.
【答案】分析:(I)根据向量数量积坐标运算公式,结合辅助角公式化简整理可得f(x)=2sin(2ωx+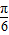 ),用三角函数周期公式即可得到ω=1,从而得到函数f(x)的解析式;
),用三角函数周期公式即可得到ω=1,从而得到函数f(x)的解析式;
(II)利用正弦函数的图象与性质,得到当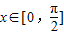 时f(x)+m的最大值为2+m,结合不等式恒成立的等价条件,即可解出实数m的取值范围.
时f(x)+m的最大值为2+m,结合不等式恒成立的等价条件,即可解出实数m的取值范围.
解答:解:(I)∵向量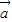 =(
=(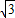 ,cos2ωx),
,cos2ωx),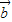 =(sin2ωx,1),(ω>0)
=(sin2ωx,1),(ω>0)
∴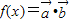 =
=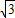 sin2ωx+cos2ωx=2sin(2ωx+
sin2ωx+cos2ωx=2sin(2ωx+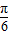 )
)
∵函数的周期T=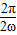 =π,∴ω=1
=π,∴ω=1
即函数f(x)的解析式是f(x)=2sin(2x+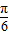 );
);
(II)当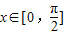 时,2x+
时,2x+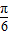 ∈[
∈[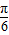 ,
,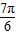 ]
]
∴- ≤sin(2ωx+
≤sin(2ωx+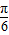 )≤1
)≤1
因此,若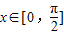 时,f(x)∈[-1,2]
时,f(x)∈[-1,2]
∴f(x)+m≤3恒成立,即2+m≤3,解之得m≤1
即实数m的取值范围是(-∞,1].
点评:本题给出向量的坐标式,求函数的表达式并讨论了函数恒成立的问题,着重考查了向量的数量积、三角恒等变换和三角函数的图象与性质等知识,属于基础题.
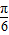 ),用三角函数周期公式即可得到ω=1,从而得到函数f(x)的解析式;
),用三角函数周期公式即可得到ω=1,从而得到函数f(x)的解析式;(II)利用正弦函数的图象与性质,得到当
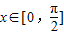 时f(x)+m的最大值为2+m,结合不等式恒成立的等价条件,即可解出实数m的取值范围.
时f(x)+m的最大值为2+m,结合不等式恒成立的等价条件,即可解出实数m的取值范围.解答:解:(I)∵向量
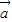 =(
=(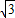 ,cos2ωx),
,cos2ωx),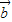 =(sin2ωx,1),(ω>0)
=(sin2ωx,1),(ω>0)∴
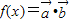 =
=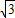 sin2ωx+cos2ωx=2sin(2ωx+
sin2ωx+cos2ωx=2sin(2ωx+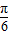 )
)∵函数的周期T=
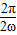 =π,∴ω=1
=π,∴ω=1即函数f(x)的解析式是f(x)=2sin(2x+
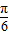 );
);(II)当
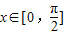 时,2x+
时,2x+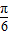 ∈[
∈[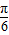 ,
,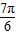 ]
]∴-
 ≤sin(2ωx+
≤sin(2ωx+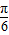 )≤1
)≤1因此,若
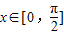 时,f(x)∈[-1,2]
时,f(x)∈[-1,2]∴f(x)+m≤3恒成立,即2+m≤3,解之得m≤1
即实数m的取值范围是(-∞,1].
点评:本题给出向量的坐标式,求函数的表达式并讨论了函数恒成立的问题,着重考查了向量的数量积、三角恒等变换和三角函数的图象与性质等知识,属于基础题.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目

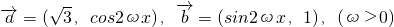 ,令
,令 ,且f(x)的周期为π.
,且f(x)的周期为π. 时f(x)+m≤3,求实数m的取值范围.
时f(x)+m≤3,求实数m的取值范围.