题目内容
已知全集U=R,设函数y=lg(x-1)的定义域为集合A,函数y=
的值域为集合B,则A∩(?∪B)=( )
| x2+2x+5 |
| A、[1,2] |
| B、[1,2] |
| C、(1,2) |
| D、(1,2) |
分析:根据负数没有对数列出不等式组,求出不等式组的解集确定出集合A,先求出x2+2x+5的值域,然后根据根式函数为增函数,根据x2+2x+5的范围即可得到
的值域,确定出集合B,最后求出两集合的交集、并集即可.
| x2+2x+5 |
解答:解:由题意得:x-1>0,解得x>1,
∴A=(1,+∞),
由x2+2x+5≥4,得到
≥2,
∴B=[2,+∞),∴?∪B=(-∞,2)
∴A∩(?∪B)=(1,2).
故选D.
∴A=(1,+∞),
由x2+2x+5≥4,得到
| x2+2x+5 |
∴B=[2,+∞),∴?∪B=(-∞,2)
∴A∩(?∪B)=(1,2).
故选D.
点评:此题属于以函数的定义域、值域为平台,考查了交集、并集的运算,要求学生熟练掌握对数的性质及根式函数的单调性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
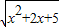 的值域为集合B,则A∩(∁∪B)=( )
的值域为集合B,则A∩(∁∪B)=( )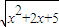 的值域为集合B,则A∩(∁∪B)=( )
的值域为集合B,则A∩(∁∪B)=( )