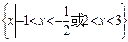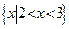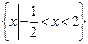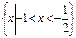题目内容
设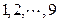 的所有排列
的所有排列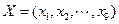 的集合为
的集合为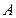 ;
;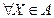 ,记
,记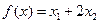
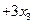
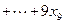 ,
,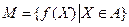 ;求
;求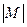 .(其中
.(其中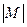 表示集合
表示集合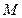 的元素个数).
的元素个数).
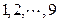 的所有排列
的所有排列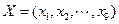 的集合为
的集合为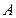 ;
;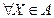 ,记
,记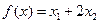
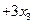
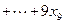 ,
,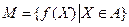 ;求
;求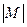 .(其中
.(其中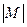 表示集合
表示集合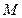 的元素个数).
的元素个数).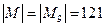
:我们一般地证明,若 ,对于前
,对于前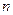 个正整数
个正整数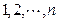 的所有排列
的所有排列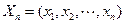 构成的集合
构成的集合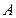 ,若
,若 ,
,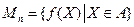 ,则
,则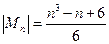 .
.
下面用数学归纳法证明: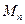
 .
.
当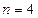 时,由排序不等式知,集合
时,由排序不等式知,集合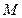 中的最小元素是
中的最小元素是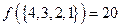 ,最大元素是
,最大元素是
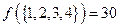 .又,
.又,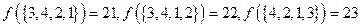 ,
,
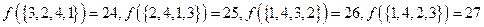 ,
,
 ,所以,
,所以,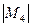 =
= 共有11=
共有11= 个元素.因此,
个元素.因此,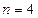 时命题成立.假设命题在
时命题成立.假设命题在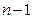 (
(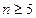 )时成立;考虑命题在
)时成立;考虑命题在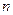 时的情况.对于
时的情况.对于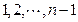 的任一排列
的任一排列 ,恒取
,恒取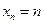 ,得到
,得到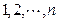 的一个排列
的一个排列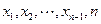 ,
,
则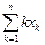
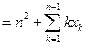 .由归纳假设知,此时
.由归纳假设知,此时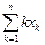 取遍区间
取遍区间
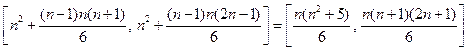 上所有整数.
上所有整数.
再令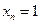 ,则
,则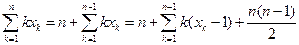
 ,
,
再由归纳假设知,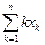 取遍区间
取遍区间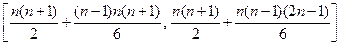
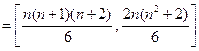 上的所有整数.
上的所有整数.
因为 ,所以,
,所以,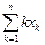 取遍区间
取遍区间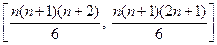
上的所有整数.即命题对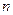 也成立.由数学归纳法知,命题成立.
也成立.由数学归纳法知,命题成立.
由于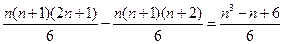 ,从而,集合
,从而,集合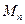
的元素个数为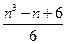 .特别是,当
.特别是,当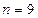 时,
时,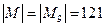 .
.
 ,对于前
,对于前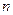 个正整数
个正整数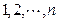 的所有排列
的所有排列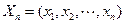 构成的集合
构成的集合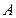 ,若
,若 ,
,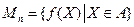 ,则
,则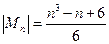 .
.
下面用数学归纳法证明:
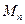
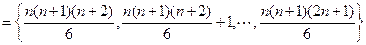 .
.当
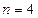 时,由排序不等式知,集合
时,由排序不等式知,集合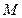 中的最小元素是
中的最小元素是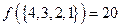 ,最大元素是
,最大元素是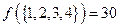 .又,
.又,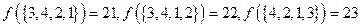 ,
,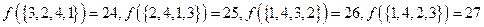 ,
, ,所以,
,所以,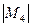 =
= 共有11=
共有11= 个元素.因此,
个元素.因此,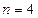 时命题成立.假设命题在
时命题成立.假设命题在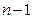 (
(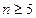 )时成立;考虑命题在
)时成立;考虑命题在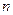 时的情况.对于
时的情况.对于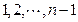 的任一排列
的任一排列 ,恒取
,恒取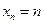 ,得到
,得到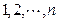 的一个排列
的一个排列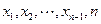 ,
,则
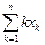
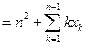 .由归纳假设知,此时
.由归纳假设知,此时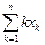 取遍区间
取遍区间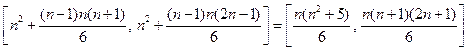 上所有整数.
上所有整数.再令
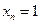 ,则
,则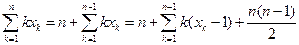
 ,
,再由归纳假设知,
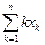 取遍区间
取遍区间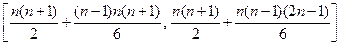
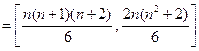 上的所有整数.
上的所有整数.因为
 ,所以,
,所以,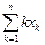 取遍区间
取遍区间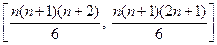
上的所有整数.即命题对
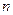 也成立.由数学归纳法知,命题成立.
也成立.由数学归纳法知,命题成立.由于
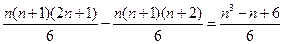 ,从而,集合
,从而,集合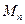
的元素个数为
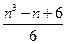 .特别是,当
.特别是,当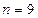 时,
时,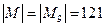 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
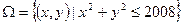 ,若点
,若点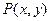 、点
、点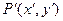 满足
满足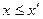 且
且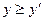 ,则称点
,则称点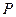 优于
优于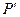 . 如果集合
. 如果集合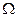 中的点
中的点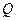 满足:不存在
满足:不存在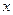 的不等式
的不等式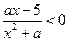 的解集为
的解集为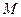 ,
,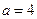 时,求解集
时,求解集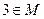 ,且
,且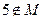 ,求实数
,求实数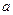 的取值范围。
的取值范围。 ,
,


 ;
; ;
;
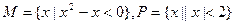 ,则
,则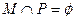
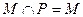
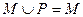
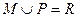
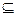 {a1, a2, a3, a4},且M∩{a1 ,a2, a3}="{" a1,a2}的集合M的个数是( )
{a1, a2, a3, a4},且M∩{a1 ,a2, a3}="{" a1,a2}的集合M的个数是( ) 。
。
 ; (2)若
; (2)若 的取值范围.
的取值范围.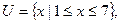
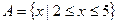 ,
,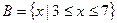 ,求:(1)
,求:(1)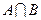 ;(2)
;(2)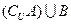
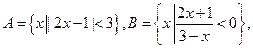 则A∩B是( )
则A∩B是( )