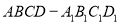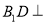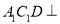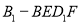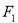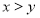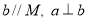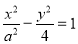题目内容
己知椭圆C: (a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线
(a>b>0)的右焦点为F(1,0),点A(2,0)在椭圆C上,过F点的直线 与椭圆C交于不同两点
与椭圆C交于不同两点 .
.
(1)求椭圆C的方程;
(2)设直线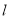 斜率为1,求线段
斜率为1,求线段 的长;
的长;
(3)设线段 的垂直平分线交
的垂直平分线交 轴于点P(0,y0),求
轴于点P(0,y0),求 的取值范围.
的取值范围.
(1)椭圆C的方程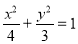 ;(2)线段
;(2)线段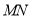 的长为
的长为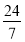 ;(3)
;(3)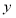 的取值范围是
的取值范围是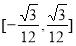 .
.
【解析】
试题分析:(1)根据椭圆的右焦点为F(1,0),点A(2,0)在椭圆C上,代入即可求得椭圆C的方程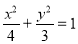 ;(2)先用点斜式
;(2)先用点斜式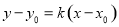 写出直线方程,再和椭圆方程联立,用弦长公式
写出直线方程,再和椭圆方程联立,用弦长公式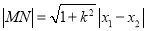 即可求出线段
即可求出线段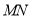 的长为
的长为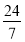 ;(3)当
;(3)当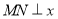 轴时,显然
轴时,显然 .当
.当 与
与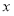 轴不垂直时,可设直线
轴不垂直时,可设直线 的方程为
的方程为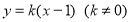 ,把直线方程与椭圆方程联立,设直线与椭圆的两个交点为
,把直线方程与椭圆方程联立,设直线与椭圆的两个交点为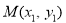 ,
, ,表示出
,表示出 ,联立即可求出
,联立即可求出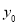 的取值范围.
的取值范围.
试题解析:(1)由题意: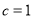 ,
,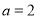 ,
,
 ,
,
所求椭圆方程为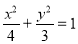 . 3分
. 3分
(2)由题意,直线l的方程为: .
.
由 得
得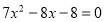 ,
,
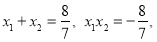
所以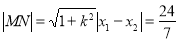 . 7分
. 7分
(3)当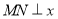 轴时,显然
轴时,显然 .
.
当 与x轴不垂直时,可设直线
与x轴不垂直时,可设直线 的方程为
的方程为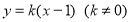 .
.
由 消去y整理得
消去y整理得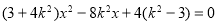 .
.
设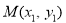 ,
, ,线段MN的中点为
,线段MN的中点为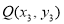 ,
,
则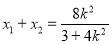 .
.
所以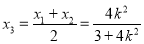 ,
,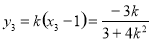
线段MN的垂直平分线方程为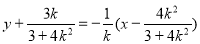
在上述方程中令x=0,得 .
.
当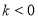 时,
时,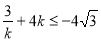 ;当
;当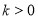 时,
时,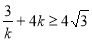 .
.
所以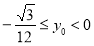 ,或
,或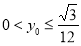 .
.
综上,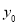 的取值范围是
的取值范围是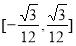 . 10分
. 10分
考点:直线与圆锥曲线的关系、函数与方程思想.

练习册系列答案
相关题目