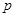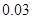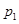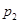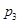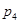题目内容
在某学校组织的一次篮球总投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分,如果前两次得分之和超过3分即停止投篮,否则投第3次.某同学在A处的命中率q1为0.25,在B处的命中率为q2.该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮的训练结束后所得的总分,其分布列为
(1)求q2的值;
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
| ξ | 0 | 2 | 3 | 4 | 5 |
| P | 0.03 | P1 | P2 | P3 | P4 |
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
分析:(1)由题设知,“ξ=0”对应的事件为“在三次投篮中没有一次投中”,由对立事件和相互独立事件性质,能求出q2.
(2)分别求出p1=p(ξ=2),p2=p(ξ=3),p3=p(ξ=4),p4=p(ξ=5),由此能求出Eξ.
(3)用C表示事件“该同学选择第一次在A处投,以后都在B处投,得分超过3分”,用D表示事件“该同学选择都在B处投,得分超过3分”,则P(C)=P(ξ=4)+P(ξ=5),P(D)=q22+
q2(1-q2),由此能求出结果.
(2)分别求出p1=p(ξ=2),p2=p(ξ=3),p3=p(ξ=4),p4=p(ξ=5),由此能求出Eξ.
(3)用C表示事件“该同学选择第一次在A处投,以后都在B处投,得分超过3分”,用D表示事件“该同学选择都在B处投,得分超过3分”,则P(C)=P(ξ=4)+P(ξ=5),P(D)=q22+
| C | 1 2 |
解答:解:(1)由题设知,“ξ=0”对应的事件为“在三次投篮中没有一次投中”,
由对立事件和相互独立事件性质,
知p(ξ=0)=(1-q1)(1-q2)2=0.03,
∵q1=0.25,
∴解得q2=0.8.
(2)根据题意p1=p(ξ=2)=(1-q1)•
(1-q2)q2=0.75×2×0.2×0.8=0.24,
p2=p(ξ=3)=q1(1-q2)2=0.25×(1-0.8)2=0.01,
p3=p(ξ=4)=(1-q1)q22=0.75×0.82=0.48,
p4=p(ξ=5)=q1q2+q1(1-q2)q2=0.25×0.8+0.25×0.2×0.8=0.24,
因此Eξ=0×0.03+2×0.24+3×0.01+4×0.48+5×0.24=3.63.
(3)用C表示事件“该同学选择第一次在A处投,以后都在B处投,得分超过3分”,
用D表示事件“该同学选择都在B处投,得分超过3分”,
则P(C)=P(ξ=4)+P(ξ=5)=P3+P4=0.48+0.24=0.72,
P(D)=q22+
q2(1-q2)=0.82+2×0.8×0.2×0.8=0.896,
故P(D)>P(C).
即该同学选择都在B处投篮得分超过3分的概率大于该同学选择第一次在A处投以后都在B处投得分超过3分的概率.
由对立事件和相互独立事件性质,
知p(ξ=0)=(1-q1)(1-q2)2=0.03,
∵q1=0.25,
∴解得q2=0.8.
(2)根据题意p1=p(ξ=2)=(1-q1)•
| C | 1 2 |
p2=p(ξ=3)=q1(1-q2)2=0.25×(1-0.8)2=0.01,
p3=p(ξ=4)=(1-q1)q22=0.75×0.82=0.48,
p4=p(ξ=5)=q1q2+q1(1-q2)q2=0.25×0.8+0.25×0.2×0.8=0.24,
因此Eξ=0×0.03+2×0.24+3×0.01+4×0.48+5×0.24=3.63.
(3)用C表示事件“该同学选择第一次在A处投,以后都在B处投,得分超过3分”,
用D表示事件“该同学选择都在B处投,得分超过3分”,
则P(C)=P(ξ=4)+P(ξ=5)=P3+P4=0.48+0.24=0.72,
P(D)=q22+
| C | 1 2 |
故P(D)>P(C).
即该同学选择都在B处投篮得分超过3分的概率大于该同学选择第一次在A处投以后都在B处投得分超过3分的概率.
点评:本题考查离散型随机变量的分布列和数学期望的求法和应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
(本小题满分12分)在某学校组织的一次篮球定点投篮训练中,规定每人最多投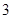 次:在
次:在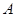 处每投进一球得
处每投进一球得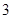 分,在
分,在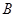 处每投进一球得
处每投进一球得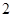 分;如果前两次得分之和超过
分;如果前两次得分之和超过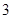 分即停止投篮,否则投第三次.某同学在
分即停止投篮,否则投第三次.某同学在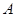 处的命中率
处的命中率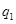 为
为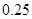 ,在
,在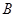 处的命中率为
处的命中率为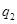 ,该同学选择先在
,该同学选择先在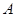 处投一球,以后都在
处投一球,以后都在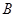 处投,用
处投,用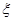 表示该同学投篮训练结束后所得的总分,其分布列为
表示该同学投篮训练结束后所得的总分,其分布列为
|
|
0 |
2 |
3 |
4 |
5 |
|
|
|
|
|
|
|
(1) 求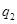 的值;
的值; (2)
求随机变量
(2)
求随机变量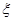 的数学期望
的数学期望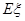 ;
;
(3) 试比较该同学选择都在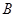 处投篮得分超过
处投篮得分超过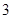 分与选择上述方式投篮得分超过
分与选择上述方式投篮得分超过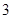 分的概率的大小.
分的概率的大小.
在某学校组织的一次篮球总投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分,如果前两次得分之和超过3分即停止投篮,否则投第3次.某同学在A处的命中率q1为0.25,在B处的命中率为q2.该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮的训练结束后所得的总分,其分布列为
(1)求q2的值;
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
| ξ | 2 | 3 | 4 | 5 | |
| P | 0.03 | P1 | P2 | P3 | P4 |
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
在某学校组织的一次篮球总投篮训练中,规定每人最多投3次;在A处每投进一球得3分,在B处每投进一球得2分,如果前两次得分之和超过3分即停止投篮,否则投第3次.某同学在A处的命中率q1为0.25,在B处的命中率为q2.该同学选择先在A处投一球,以后都在B处投,用ξ表示该同学投篮的训练结束后所得的总分,其分布列为
(1)求q2的值;
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.
| ξ | 2 | 3 | 4 | 5 | |
| P | 0.03 | P1 | P2 | P3 | P4 |
(2)求随机变量ξ的数学期望Eξ;
(3)试比较该同学选择在B处投篮得分超过3分与选择上述方式投篮得分超过3分的概率的大小.