题目内容
已知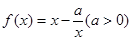 ,
,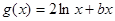 ,且直线
,且直线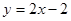 与曲线
与曲线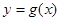 相切.
相切.
(1)若对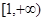 内的一切实数
内的一切实数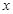 ,不等式
,不等式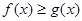 恒成立,求实数
恒成立,求实数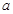 的取值范围;
的取值范围;
(2)(ⅰ)当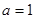 时,求最大的正整数
时,求最大的正整数 ,使得任意
,使得任意 个实数
个实数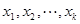
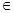
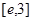 (
(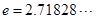 是自然对数的底数)都有
是自然对数的底数)都有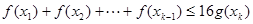 成立;
成立;
(ⅱ)求证: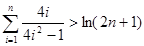
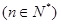 .
.
【答案】
(1)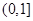 ;(2)(ⅰ)13;(ⅱ)详见解析.
;(2)(ⅰ)13;(ⅱ)详见解析.
【解析】
试题分析:(1)由直线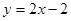 与曲线
与曲线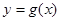 相切可以求出
相切可以求出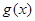 中的参数
中的参数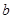 .再由对
.再由对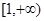 内的一切实数
内的一切实数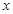 ,不等式
,不等式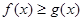 恒成立,即
恒成立,即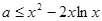 在
在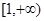 上恒成立,然后构造函数
上恒成立,然后构造函数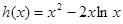 ,研究其导函数以确定其单调性,从而得到其最小值1.又
,研究其导函数以确定其单调性,从而得到其最小值1.又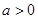 ,所以实数
,所以实数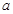 的取值范围是
的取值范围是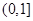 ;(2)(ⅰ)先通过导函数确定
;(2)(ⅰ)先通过导函数确定 在
在 上是增函数,从而得到
上是增函数,从而得到 在
在 上的最大值.由题意,必须使得不等式左边的最大值小于或等于右边的最小值.经计算知
上的最大值.由题意,必须使得不等式左边的最大值小于或等于右边的最小值.经计算知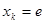 时不等式右边取得最小值,然后代入不等式,解得
时不等式右边取得最小值,然后代入不等式,解得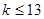 .因此,
.因此, 的最大值为
的最大值为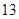 ;(ⅱ)根据(1)的推导
;(ⅱ)根据(1)的推导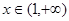 时,
时,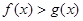 ,从而
,从而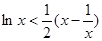 ,再通过令
,再通过令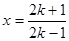 代入化简即可得证.
代入化简即可得证.
试题解析:(1)设点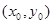 为直线
为直线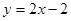 与曲线
与曲线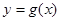 的切点,则有
的切点,则有
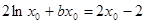 . (*)
. (*)
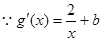 ,
,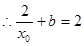 . (**)
. (**)
由(*)、(**)两式,解得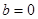 ,
,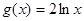 . 1分
. 1分
由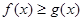 整理,得
整理,得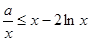 ,
,
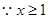 ,
, 要使不等式
要使不等式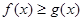 恒成立,必须
恒成立,必须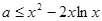 恒成立. 2分
恒成立. 2分
设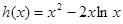 ,
,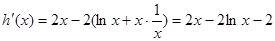 ,
,
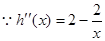 ,
,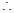 当
当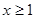 时,
时,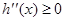 ,则
,则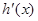 是增函数,
是增函数,
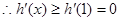 ,
,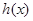 是增函数,
是增函数,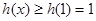 ,
,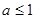 .
.
因此,实数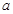 的取值范围是
的取值范围是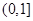 . 4分
. 4分
(2)(ⅰ)当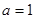 时,
时, ,
,
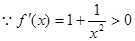 ,
,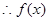 在
在 上是增函数,
上是增函数,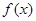 在
在 上的最大值为
上的最大值为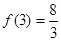 .
.
要对 内的任意
内的任意 个实数
个实数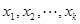 都有
都有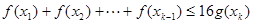
成立,必须使得不等式左边的最大值小于或等于右边的最小值,
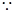 当
当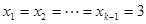 时不等式左边取得最大值,
时不等式左边取得最大值,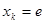 时不等式右边取得最小值.
时不等式右边取得最小值.
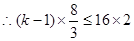 ,解得
,解得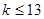 .因此,
.因此, 的最大值为
的最大值为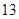 . 8分
. 8分
(ⅱ)证明:当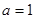 时,根据(1)的推导有,
时,根据(1)的推导有,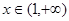 时,
时,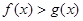 ,
,
即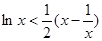 .令
.令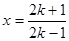 ,得
,得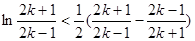 ,
,
化简得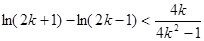 ,
,
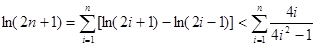 . 13分
. 13分
考点:1.用导数研究函数的单调性;2.函数的单调性与最值;3.不等式.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
 ,
,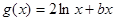 ,且直线
,且直线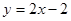 与曲线
与曲线 相切.
相切. 内的一切实数
内的一切实数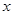 ,不等式
,不等式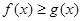 恒成立,求实数
恒成立,求实数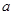 的取值范围;
的取值范围;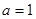 时,求最大的正整数
时,求最大的正整数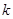 ,使得对
,使得对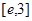 (
(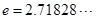 是自然对数的底数)内的任意
是自然对数的底数)内的任意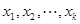 都有
都有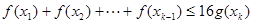 成立;
成立;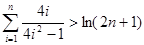
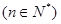 .
. 直线
直线 ,且直线
,且直线 与曲线
与曲线 相切于点
相切于点 ,求直线
,求直线 的坐标。
的坐标。