题目内容
设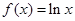 ,
,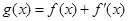 .
.
(1)求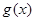 的单调区间和最小值;
的单调区间和最小值;
(2)讨论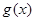 与
与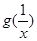 的大小关系;
的大小关系;
(3)求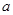 的取值范围,使得
的取值范围,使得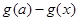 <
<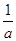 对任意
对任意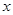 >0成立
>0成立
【答案】
【解】(1)由题设知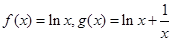 ,∴
,∴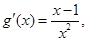 令
令 0得
0得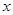 =1,
=1,
当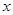 ∈(0,1)时,
∈(0,1)时,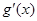 <0,
<0,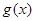 是减函数,故(0,1)是
是减函数,故(0,1)是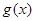 的单调减区间。
的单调减区间。
当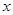 ∈(1,+∞)时,
∈(1,+∞)时,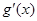 >0,
>0,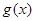 是增函数,故(1,+∞)是
是增函数,故(1,+∞)是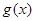 的单调递增区间,
的单调递增区间,
因此,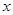 =1是
=1是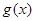 的唯一极值点,且为极小值点,从而是最小值点,所以
的唯一极值点,且为极小值点,从而是最小值点,所以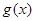 的最小值为
的最小值为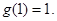
(2)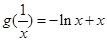 ,设
,设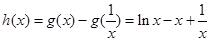 ,则
,则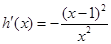 ,
,
当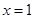 时,
时,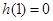 ,即
,即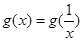 ,当
,当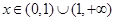 时,
时,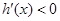 ,
,
因此,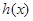 在
在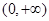 内单调递减,当
内单调递减,当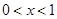 时,
时,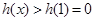 ,即
,即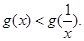
(3)由(1)知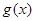 的最小值为1,所以,
的最小值为1,所以,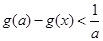 ,对任意
,对任意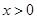 ,成立
,成立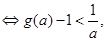
即 从而得
从而得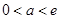 。
。
【解析】略

练习册系列答案
相关题目
 上的一点,以
上的一点,以 轴的非负半轴为始边、OP为终边的角记为
轴的非负半轴为始边、OP为终边的角记为 ,又向量
,又向量 。且
。且 .
. 的单调减区间;
的单调减区间; 的方程
的方程 在
在 内有两个不同的解,求
内有两个不同的解,求 的取值范围.
的取值范围. ,
,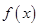 的反函数
的反函数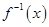 ;
;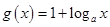 ,当
,当
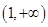 ,
,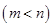 时,
时,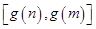 ,求
,求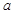 的取值范围.
的取值范围. ,(1)求
,(1)求 的振幅,周期和初相;(2)求
的振幅,周期和初相;(2)求 值组成的集合。(3)求
值组成的集合。(3)求