题目内容
5.(1)已知p:-x2+8x+20≥0,q:x2-2x+1-m2≤0(m>0).若“¬p”是“¬q”的充分不必要条件,求实数m的取值范围;(2)已知两个关于x的一元二次方程mx2-4x+4=0和x2-4mx+4m2-4m-5=0,求两方程的根都是整数的充要条件.
分析 (1)先求出p,q为真时的x的范围,根据q是p的充分不必要条件得到关于m的不等式组,解出即可;
(2)根据方程根的情况结合二次函数的性质求出m的范围,取交集即可.
解答 解:(1)p:-2≤x≤10,q:1-m≤x≤1+m.-----(2分)
∵“非p”是“非q”的充分不必要条件,∴q是p的充分不必要条件.
∴$\left\{\begin{array}{l}{m>0}\\{1-m≥-2}\\{1+m≤10}\end{array}\right.$,∴0<m≤3.
∴实数m的取值范围为0<m≤3.-------(6分)
(2)∵mx2-4x+4=0是一元二次方程,∴m≠0.
又另一方程为x2-4mx+4m2-4m-5=0,且两方程都要有实根,
∴$\left\{\begin{array}{l}△1=16(1-m)≥0\\△2=16m2-4(4m2-4m-5)≥0\end{array}$,
解得m∈[-$\frac{5}{4}$,1]----(8分)
∵两方程的根都是整数,故其根的和与积也为整数,
∴$\left\{\begin{array}{l}\frac{4}{m}∈Z\\ 4m∈Z,4m2-4m-5∈Z.\end{array}$
∴m为4的约数.又∵m∈[-$\frac{5}{4}$,1],∴m=-1或1.
当m=-1时,第一个方程x2+4x-4=0的根为非整数;
而当m=1时,两方程的根均为整数,
∴两方程的根均为整数的充要条件是m=1.-----(12分)
点评 本题考查了充分必要条件,考查方程根的情况,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.已知函数f(x)=sin2x,为了得到g(x)=cos2x的图象,只要将y=f(x)的图象( )
| A. | 向左平移$\frac{π}{2}$个单位长度 | B. | 向右平移$\frac{π}{2}$个单位长度 | ||
| C. | 向左平移$\frac{π}{4}$个单位长度 | D. | 向右平移$\frac{π}{4}$个单位长度 |
20.20152015除以8的余数为( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
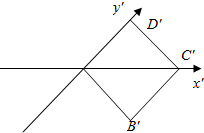 如图,A′B′C′D′是边长为1的正方形,又知它是某个四边形按斜二测画法画出的直观图,请画出该四边形的原图形,并求出原图形面积.
如图,A′B′C′D′是边长为1的正方形,又知它是某个四边形按斜二测画法画出的直观图,请画出该四边形的原图形,并求出原图形面积.