题目内容
(本小题满分10分)选修4-5:不等式选讲。设函数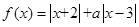
(Ⅰ)当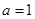 时,求函数
时,求函数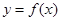 的最小值,并指出取得最小值时
的最小值,并指出取得最小值时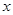 的值;
的值;
(Ⅱ)若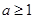 ,讨论关于
,讨论关于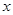 的方程
的方程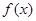 =
=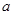 的解的个数.
的解的个数.
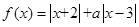
(Ⅰ)当
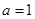 时,求函数
时,求函数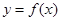 的最小值,并指出取得最小值时
的最小值,并指出取得最小值时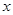 的值;
的值;(Ⅱ)若
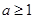 ,讨论关于
,讨论关于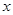 的方程
的方程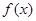 =
=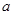 的解的个数.
的解的个数.解:(Ⅰ)∵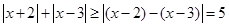
∴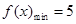 ,当且仅当
,当且仅当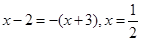 时
时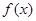 取最小值 ………4分
取最小值 ………4分
(2)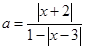 ,设
,设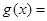
 ,则
,则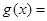
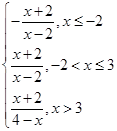 ,
,
画出其图象可知,当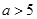 时,原方程有2个解;当
时,原方程有2个解;当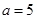 时,原方程有1个解;
时,原方程有1个解;
当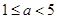 时,原方程无解 ……………………………10分
时,原方程无解 ……………………………10分
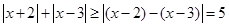
∴
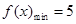 ,当且仅当
,当且仅当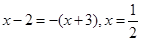 时
时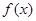 取最小值 ………4分
取最小值 ………4分(2)
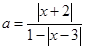 ,设
,设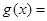
 ,则
,则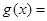
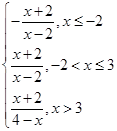 ,
,画出其图象可知,当
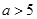 时,原方程有2个解;当
时,原方程有2个解;当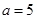 时,原方程有1个解;
时,原方程有1个解;当
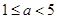 时,原方程无解 ……………………………10分
时,原方程无解 ……………………………10分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
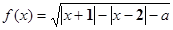 ,若函数
,若函数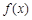 的定义域为
的定义域为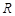 ,则实数
,则实数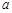 的取值范围是 .
的取值范围是 . .(I)求不等式
.(I)求不等式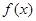 ≤6的解集;(Ⅱ)若关于
≤6的解集;(Ⅱ)若关于 的不等式
的不等式 恒成立,求实数
恒成立,求实数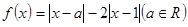 .
.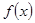 的最大值;
的最大值;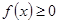
 ;
; 的不等式
的不等式 有解,求实数
有解,求实数 的取值范围.
的取值范围.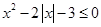 的解集为
的解集为 
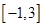
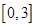
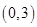
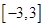
 ,不等式
,不等式 的解集为M.
的解集为M. 时,证明:
时,证明: .
. 的最小值为( )
的最小值为( )
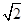


 ≤1的解集
≤1的解集 。
。