题目内容
为了体现国家“民生工程”,某市政府为保障居民住房,现提供一批经济适用房.现有条件相同的甲、已、丙、丁四套住房供A、B、C三人自主申请,他们的申请是相互独立的.(Ⅰ)求A、B两人都申请甲套住房的概率;
(Ⅱ)求A、B两人不申请同一套住房的概率;
(Ⅲ)设3名参加选房的人员中选择甲套住房的人数为ξ,求ξ的分布列和数学期望.
【答案】分析:(Ⅰ)设“A申请甲套住房”为事件M1,“B申请甲套住房”为事件M2.由事件A和B是独立事件,能求出A,B两人都申请甲套住房的概率.
(Ⅱ)设“A,B两人选择同一套住房”为事件N,先求出事件N的概率,再求A,B两人不选择同一套住房的概率.
(Ⅲ)法一:随机变量ξ可能取的值为0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列和Eξ.
法二:依题意得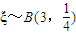 ,由此能求出ξ的分布列和Eξ.
,由此能求出ξ的分布列和Eξ.
解答:(本小题满分12分)
解:(Ⅰ)设“A申请甲套住房”为事件M1,“B申请甲套住房”为事件M2
那么A,B两人都申请甲套住房的概率

所以甲、乙两人都申请甲套住房的概率为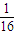 …(3分)
…(3分)
(Ⅱ)设“A,B两人选择同一套住房”为事件N,

所以A,B两人不选择同一套住房的概率是
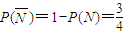 …(7分)
…(7分)
(Ⅲ)(方法一)随机变量ξ可能取的值为0,1,2,3,那么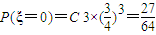 ;
;
 ;
;
 ;
;
 ;
;
所以ξ的分布列为
…(11分)
所以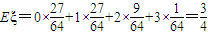 …(12分)
…(12分)
(方法二)依题意得
所以ξ的分布列为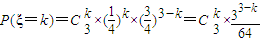 ,k=0,1,2,3.
,k=0,1,2,3.
即
…(11分)
所以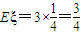 …(12分)
…(12分)
点评:本题考查离散型随机变量的分布列和数学期望,是中档题.在历年高考中都是必考题型.解题时要认真审题,仔细解答,注意概率知识的合理运用.
(Ⅱ)设“A,B两人选择同一套住房”为事件N,先求出事件N的概率,再求A,B两人不选择同一套住房的概率.
(Ⅲ)法一:随机变量ξ可能取的值为0,1,2,3,分别求出P(ξ=0),P(ξ=1),P(ξ=2),P(ξ=3),由此能求出ξ的分布列和Eξ.
法二:依题意得
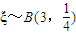 ,由此能求出ξ的分布列和Eξ.
,由此能求出ξ的分布列和Eξ.解答:(本小题满分12分)
解:(Ⅰ)设“A申请甲套住房”为事件M1,“B申请甲套住房”为事件M2
那么A,B两人都申请甲套住房的概率

所以甲、乙两人都申请甲套住房的概率为
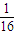 …(3分)
…(3分)(Ⅱ)设“A,B两人选择同一套住房”为事件N,

所以A,B两人不选择同一套住房的概率是
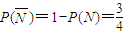 …(7分)
…(7分)(Ⅲ)(方法一)随机变量ξ可能取的值为0,1,2,3,那么
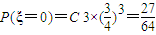 ;
; ;
; ;
; ;
;所以ξ的分布列为
| ξ | 1 | 2 | 3 | |
| P | 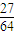 |  | 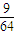 | 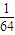 |
所以
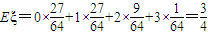 …(12分)
…(12分)(方法二)依题意得

所以ξ的分布列为
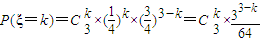 ,k=0,1,2,3.
,k=0,1,2,3.即
| ξ | 1 | 2 | 3 | |
| P |  | 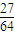 | 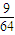 | 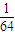 |
所以
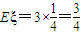 …(12分)
…(12分)点评:本题考查离散型随机变量的分布列和数学期望,是中档题.在历年高考中都是必考题型.解题时要认真审题,仔细解答,注意概率知识的合理运用.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目