题目内容
在正三棱锥P-ABC中,三条侧棱两两互相垂直,G是△PBA的重心,E,F分别是BC,PB上的点,且 .(1)求证:平面GEF⊥平面PBC;(2)求证:GE是PG,BC的公垂线.
.(1)求证:平面GEF⊥平面PBC;(2)求证:GE是PG,BC的公垂线.

答案:
解析:
解析:
|
证 (1)∵PA⊥PB,PA⊥PC,∴PA⊥平面PBC.连BG并延长交PA于M.∵G是△PBA的重心,∴ (2)取EC的中点D,连FD,∵ |

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
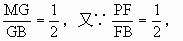 ∴
∴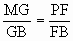 ,故GF∥PA.因此GF⊥平面PBC,∴平面GFE⊥平面PBC.
,故GF∥PA.因此GF⊥平面PBC,∴平面GFE⊥平面PBC.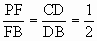 ,∴FD∥PC,由PC=PB可得FD=FB,E是BD的中点,∴EF⊥BC,∵GF⊥平面PBC,∴EF是GE在平面PBC内的射影,于是GE⊥BC.取FB的中点N,连GN,∵G是△PAB的重心,设PG交AB于Q,于是
,∴FD∥PC,由PC=PB可得FD=FB,E是BD的中点,∴EF⊥BC,∵GF⊥平面PBC,∴EF是GE在平面PBC内的射影,于是GE⊥BC.取FB的中点N,连GN,∵G是△PAB的重心,设PG交AB于Q,于是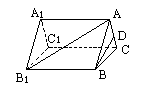

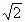




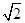 ,
, ,点E、F分别在侧棱PB、PC上,则
,点E、F分别在侧棱PB、PC上,则 周长的最小值为 .
周长的最小值为 . ,
, ,点E、F分别在侧棱PB、PC上,则
,点E、F分别在侧棱PB、PC上,则 周长的最小值为 .
周长的最小值为 .