有一块草地为菱形.在菱形的对角线交点处有一根垂直于草地的旗杆.若该菱形面积为240m2.周长为80m.旗杆高为8m.则旗杆顶端到菱形边的最短距离为( )A．6mB．8mC．10mD．12m 题目和参考答案——青夏教育精英家教网—

题目内容

6．有一块草地为菱形，在菱形的对角线交点处有一根垂直于草地的旗杆，若该菱形面积为240m²，周长为80m，旗杆高为8m，则旗杆顶端到菱形边的最短距离为（　　）

A．

B．

C．

10m

D．

12m

分析画出图形，求出底面菱形的对角线交点到边的距离，利用勾股定理求解即可．

解答解：菱形的对角线交点处有一根垂直于草地的旗杆，若该菱形面积为240m²，周长为80m，可得AB=BC=CD=DA=20，PO=8，
过O作OE⊥AB，连结PE，
S_ABCD=$4×\frac{1}{2}AB×OE$=4×$\frac{1}{2}×20×OE$=240，
可得OE=6．
PE=$\sqrt{{PO}^{2}+{OE}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10（m）．
故选：C．

点评本题考查空间几何体的点线面的距离的求法，考查空间想象能力以及计算能力．

练习册系列答案

红色风暴初中生学业考试模拟与预测系列答案

鸿图图书寒假作业假期作业吉林大学出版社系列答案

中考新概念系列答案

互联网多功能作业本系列答案

相关题目

6．下列命题中正确的是（　　）

	A．	命题“?x∈R，x²-x≤0”的否定是“?x∈R，x²-x≥0”
	B．	命题“p∧q为真”是命题“p∨q为真”的必要不充分条件
	C．	若“am²≤bm²，则a≤b”的否命题为真
	D．	若实数x，y∈[-1，1]，则点（x，y）所构成的平面区域为π

7．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为45°，且$\overrightarrow{a}$=（2，-2），|$\overrightarrow{b}$|=1，则|$\overrightarrow{a}$-$\overrightarrow{b}$|=（　　）

4．设f₀（x）=sinx，f₁（x）=f′₀（x），f₂（x）=f′₁（x），…，f_n+1（x）=f′_n（x），n∈N，试求f₂₀₁₄（x）．

1．设数列{a_n}的前n项和为S_n，p，q是与n无关的常数．
（1）若$\frac{{S}_{n}}{n}$=pn+q（n∈N^*），且$\frac{1}{3}$S₃与$\frac{1}{4}$S₄的等差中项为1，而$\frac{1}{5}$S₅是$\frac{1}{3}$S₃与$\frac{1}{4}$S₄的等比中项，求数列{a_n}的通项公式；
（2）若$\frac{{S}_{n}}{{a}_{n}}$=pn+q（n∈N^*），是否存在p，q，使得数列{a_n}为等差数列？若存在，求出p，q的值；若不存在，请说明理由．

11．某班班会，准备从包括甲、乙两人的七名同学中选派4名学生发言，要求甲、乙两人中至少有1人参加，则甲、乙都被选中且发言时不相邻的概率为$\frac{1}{7}$．

18．

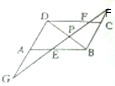如图，四边形ABCD是平行四边形，P是BD上任意一点，过P点的直线分别交AB，DC于E，F，交DA，BC的延长线于G，H．
（1）求证：PE•PG=PF•PH；
（2）当过P点的直线绕点P旋转到F，H，C重合时，请判断PE、PC、PG的关系，并给出证明．

15．设点（x₀，0）在函数f（x）=3sin（x-$\frac{π}{3}$）-1的图象上，其中$\frac{5π}{6}$＜x₀＜$\frac{4π}{3}$，则cos（x₀-$\frac{π}{6}$）的值为-$\frac{2\sqrt{6}+1}{6}$．

16．已知以点C（1，-3）为圆心的圆C截直线4x-3y+2=0得到的弦长等于2，椭圆E的长轴长为6，中心为原点，椭圆E的焦点为F₁，F₂，点P在椭圆E上，△F₁PF₂是直角三角形，若椭圆E的一个焦点是圆C与坐标轴的一个公共点，则点P到x轴的距离为$\frac{5}{3}$．

试题分类