题目内容
若∆ABC的三个内角成等差数列,三边成等比数列,则∆ABC是
| A.直角三角形 | B.等腰直角三角形 | C.等边三角形 | D.钝角三角形 |
C
解析试题分析:根据三内角成等差,设A,B,C成等差,则有A+B+C=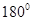 ,
,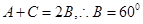 ,进而结合三边的比例,则有
,进而结合三边的比例,则有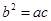 ,通过余弦定理
,通过余弦定理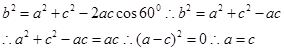
因此可知A=C,故可知三角形为等边三角形,选C
考点:本试题主要是考查了等差数列和等比数列的性质的运用。
点评:解决该试题的关键是,根据三内角成等差,说明了有个角为60度,进而结合三边的比例,想到用余弦定理求解。

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
在相距2千米的 .
. 两点处测量目标
两点处测量目标 ,若
,若 ,则
,则 ,
, 两点之间的距离是( )千米.
两点之间的距离是( )千米.
| A.1 | B. | C. | D. 2 |
在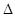 ABC中,
ABC中,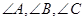 所对的边分别为a,b,c,已知a=2,b=
所对的边分别为a,b,c,已知a=2,b=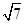 ,
,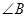 =
= ,则
,则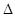 ABC的面积为
ABC的面积为
A.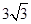 | B.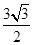 | C. | D.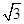 |
已知等腰三角形腰上的中线长为 ,则该三角形的面积的最大值为( )
,则该三角形的面积的最大值为( )
A. | B. | C. | D. |
.已知直线 与圆
与圆 相离,则三条边长分别为
相离,则三条边长分别为 、
、 、
、 的三角形是
的三角形是
| A.锐角三角形 | B.直角三角形 | C.钝角三角形 | D.以上均有可能 |
已知 中,
中,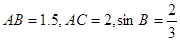 .则
.则 ( )。
( )。
A. | B. | C. 或 或 | D. 或 或 |
已知 中,
中, 则
则 等于( )
等于( )
A. | B. | C. | D. |
在△ 中,若
中,若 ,则△
,则△ 的形状是( )
的形状是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.不能确定 |
 ,则△ABC的面积S =
,则△ABC的面积S =