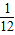题目内容
一名同学先后投掷一枚骰子两次,第一次向上的点数记为x,第二次向上的点数记为y,在直角坐标系xOy中,以(x,y)为坐标的点落在直线2x+y=8上的概率为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
分析:本题是一个古典概型,试验发生包含的事件是先后掷两次骰子,共有6×6种结果,满足条件的事件是(x,y)为坐标的点落在直线2x+y=8上,列举当x=1,y=6;x=2,y=4;x=3,y=2,共有3种结果,得到概率.
解答:解:由题意知本题是一个古典概型,
∵试验发生包含的事件是先后掷两次骰子,共有6×6=36种结果,
满足条件的事件是(x,y)为坐标的点落在直线2x+y=8上,
当x=1,y=6;x=2,y=4;x=3,y=2,共有3种结果,
∴根据古典概型的概率公式得到P=
=
,
故选B.
∵试验发生包含的事件是先后掷两次骰子,共有6×6=36种结果,
满足条件的事件是(x,y)为坐标的点落在直线2x+y=8上,
当x=1,y=6;x=2,y=4;x=3,y=2,共有3种结果,
∴根据古典概型的概率公式得到P=
| 3 |
| 36 |
| 1 |
| 12 |
故选B.
点评:本题考查古典概型的概率公式,考查满足直线方程的点,考查利用列举法得到事件数,本题是一个基础题,适合文科学生做,列举时注意要以x为主来讨论.

练习册系列答案
相关题目
 ,第二次向上的点数记为
,第二次向上的点数记为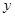 ,在直角坐标系
,在直角坐标系 中,以
中,以 为坐标的点落在直线
为坐标的点落在直线 上的概率为 ( )
上的概率为 ( )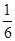 B.
B. C.
C. D.
D.