题目内容
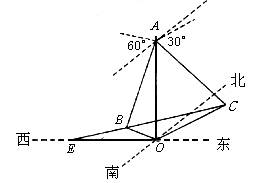
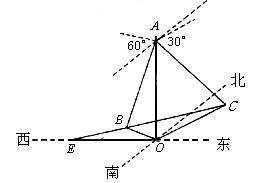
在海岛O上有一座海拔1千米的山，山顶设有一个观察站A，上午11时，测得一轮船在岛北60°东，俯角为30°的C处，到11时10分，又测得该船在岛北60°西，俯角为60°的B处，（如图）．求：
（1）船的航行速度；
（2）又经过一段时间后，船到达海岛O的正西方向的E处，问此时船距岛O有多远?
答案：
解析：
解析：
解（1）由已知，在RtDABO中，OB=OA×cot60°= OC=OA×cot30°= BC2=OB2+OC2-2×OB×OC×cosÐBOC= ∴ BC= ∴ 船速
（2）在DBOC中，由余弦定理得 ∴ sinÐBEO=sin[180°-(30°+ÐEBO)] =(30°+ÐEBO)
= 在DBOE中，由正弦定理得 ∴ BE= 于是从B至E所需时间 此时 ∴ 船在11时15分到达海岛正西方向，此时点E离开工海岛1.5km． |
(km)；在DACO中，
(km)；在DBOC中，由余弦定理得
+3-2´
cos120°=
．
(km)，∵ 船从C行到B用去10min=
h，
，sinÐOBC=
，
(km)
．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
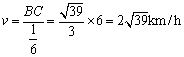
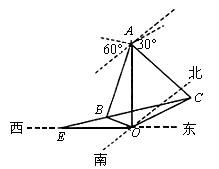
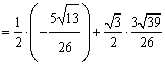
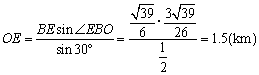
海岛O上有一座海拔1000米的山，山顶上设有一个观察站A，上午11时，测得一轮船在岛北偏东60°C处，俯角30°，11时10分，又测得该船在岛的北偏西60°西B处，俯角60°．
