题目内容
素材1:上午11时测得一轮船在海岛O北偏东60°的C处,俯角为30°;素材2:海岛O上有一座海拔1 000 m高的山,山顶上设有一个观察站A;
素材3:上午11时30分测得轮船在岛的北偏西60°的B处,俯角为60°.
将上面的素材构建成一个问题,然后再解答.
构建问题:
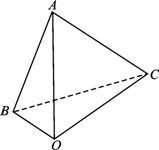
如下图,海岛O上有一座海拨1 000 m高的山,山顶上设有一个观察站A.上午11时测得一轮船在岛北偏东60°的C处,俯角为30°;11时30分又测得该船在岛的北偏西60°的B处,俯角为60°,求该船的航行速度.
解析:该船从C处到达B处用时![]() h,故欲求其速度关键是求出BC的长.
h,故欲求其速度关键是求出BC的长.
AO⊥平面OBC,在△AOC中,∠AOC=90°,AO=1 000,∠OAC=60°,∴OC=1 000![]() .在△AOB中,∠AOB=90°,AO=1 000,∠OAB=30°,∴OB=
.在△AOB中,∠AOB=90°,AO=1 000,∠OAB=30°,∴OB=![]() .
.
在△OBC中,∠BOC=120°,
由余弦定理BC2=OC2+OB2-2OC·OB·cos120°=![]() ,
,
∴BC=![]() .
.
故该船的速度为![]() (m/h).
(m/h).

练习册系列答案
相关题目