题目内容

已知函数ft(x)=(x-t)2-t（t∈R），设a＜b，f(x)=
fa(x)，fa(x)＜fb(x)
fb(x)，fa(x)≥fb(x)
，若函数f（x）+x+a-b有四个零点，则b-a的取值范围是（　　）
分析：解方程fa（x）=fb（x）得交点P(
a+b-1
2
，(
b-a-1
2
)2-a)，函数f（x）的图象与直线l：y=-x+b-a有四个不同的交点，由图象知，点P在l的上方，故
a+b-1
2
+(
b-a-1
2
)2-a-(b-a)＞0，由此解得b-a的取值范围．
解答：解：作函数f（x）的图象，且解方程fa（x）=fb（x）得x=
a+b-1
2
，即交点P(
a+b-1
2
，(
b-a-1
2
)2-a)，
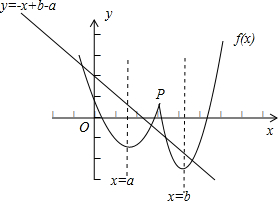
又函数f（x）+x+a-b有四个零点，即函数f（x）的图象与直线l：y=-x+b-a有四个不同的交点．
由图象知，点P在l的上方，所以
a+b-1
2
+(
b-a-1
2
)2-a-(b-a)＞0，解得b-a＞2+
5
．
故选C．
点评：本题主要考查根的存在性以及根的个数判断，函数的零点与方程的根的关系，体现了转化的数学思想，属于中档题．
练习册系列答案
相关题目
（2013•宜宾二模）已知函数ft（x）=
1
1+x
-
1
(1+x)2
（t-x），其中t为正常数．
（Ⅰ）求函数ft（x）在（0，+∞）上的最大值；
（Ⅱ）设数列{an}满足：a1=
5
3
，3an+1=an+2，（1）求数列{an}的通项公式an； （2）证明：对任意的x＞0，
1
an
≥f
2
3n
（x）（n∈N*）；
（Ⅲ）证明：
1
a1
+
1
a2
+…+
1
an
＞
n2
n+1
．
已知函数ft(x)=
1
1+x
-
1
(1+x)2
(t-x)，其中t为常数，且t＞0．
（Ⅰ）求函数ft（x）在（0，+∞）上的最大值；
（Ⅱ）数列{an}中，a1=
2
3
，an+1an=2an-an+1，求{an}的通项公式；
（Ⅲ）证明：对任意的x＞0，an≥f
1
2n
(x)，n=1，2，…．
已知函数ft(x)=
1
1+x
-
1
(1+x)2
(t-x)，其中t为常数，且t＞0．
（Ⅰ）求函数ft（x）在（0，+∞）上的最大值；
（Ⅱ）数列{an}中，a1=3，a2=5，其前n项和Sn满足Sn+Sn-2=2Sn-1+2n-1（n≥3），且设bn=1-
1
an
，证明：对任意的x＞0，bn≥f
1
2n
(x)，n=1，2，…．
已知函数ft（x）=（t-x），其中t为正常数．
（Ⅰ）求函数ft（x）在（0，+∞）上的最大值；
（Ⅱ）设数列{an}满足：a1=，3an+1=an+2，（1）求数列{an}的通项公式an； （2）证明：对任意的x＞0，（x）（n∈N*）；
（Ⅲ）证明：．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网