题目内容
设两个向量e1,e2,满足|e1|=2,|e2|=1,e1与e2的夹角为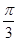 .若向量2te1+7e2与e1+te2的夹角为钝角,求实数t的范围.
.若向量2te1+7e2与e1+te2的夹角为钝角,求实数t的范围.
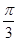 .若向量2te1+7e2与e1+te2的夹角为钝角,求实数t的范围.
.若向量2te1+7e2与e1+te2的夹角为钝角,求实数t的范围.-7<t<-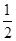 且t≠-
且t≠-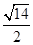
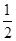 且t≠-
且t≠-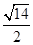
【错解分析】∵2te1+7e2与e1+te2的夹角为钝角,
∴(2te1+7e2)·(e1+te2)<0,
∴2t2+15t+7<0,解之得:-7<t<-
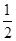 ,
,∴t的范围为(-7,-
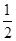 ).
).【正解】∵2te1+7e2与e1+te2的夹角为钝角,
∴(2te1+7e2)·(e1+te2)<0且2te1+7e2≠λ(e1+te2)(λ<0).
∵(2te1+7e2)·(e1+te2)<0得2t2+15t+7<0,
∴-7<t<-
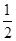 .
.若2te1+7e2=λ(e1+te2)(λ<0),
∴(2t-λ) e1+(7-tλ) e2=0.
∴
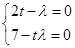 ,即t=-
,即t=-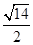 ,
,∴t的取值范围为:-7<t<-
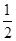 且t≠-
且t≠-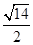 .
.【点评】本题错误的关键是没有把握准向量夹角与向量数量积的等价关系.一般地,向量a,b为非零向量,a与b的夹角为θ,则①θ为锐角?a·b>0且a, b不同向;②θ为直角?a·b=0;③θ为钝角?a·b<0且a·b不反向.
2te1+7e2与e1+te2的夹角为钝角?(2te1+7e2)·(e1+te2)<0.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 ,
,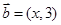 ,且
,且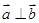 ,则实数
,则实数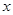 的值为
的值为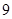
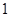
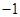
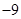
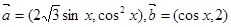 ,函数
,函数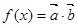
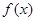 的单调递减区间.
的单调递减区间.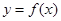 的图象向左平移
的图象向左平移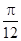 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的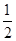 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数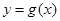 的图象.求
的图象.求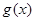 在
在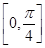
 上的值域.
上的值域.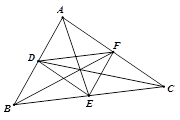
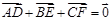
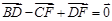
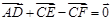
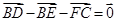
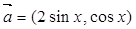
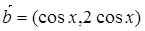
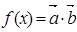 并求
并求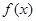 的单调递增区间。
的单调递增区间。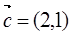 ,且
,且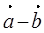 与
与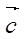 共线,
共线,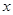 为第二象限角,求
为第二象限角,求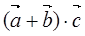 的值。
的值。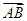 =
=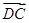 =(1,1),
=(1,1),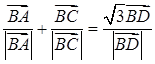 ,则四边形ABCD的面积是
,则四边形ABCD的面积是 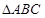 ,点
,点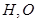 为
为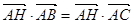 ,
,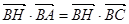 ,
, 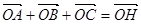 , 则点O为
, 则点O为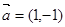 ,
,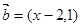 ,且
,且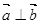 ,则实数
,则实数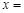
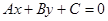 (其中
(其中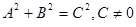 )与圆
)与圆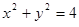 交于
交于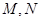 ,O是坐标原点,则
,O是坐标原点,则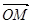 ·
·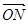 =( )
=( ) 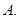 2
2 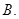 1
1 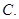 -1
-1  -2
-2