题目内容
(重点中学做) 用二分法求函数f(x)=
-x-cosx(x>0)在区间[0,2π]内的零点,二分区间[0,2π]的次数为( )
| π |
| 2 |
分析:先由导数工具可以证出函数f(x)在(0,+∞)上是单调减函数,在(0,+∞)上零点个数不超过一个.再根据零点存在性定理,判断每个选项中两端点的函数值之积是否小于0,因此要计算出f(0)>0,f(2π)<0,f(π)<0,f(
)=0即可得出正确答案.
| π |
| 2 |
解答:解:可以利用导数工具求得
f /(x)= (
-x-cosx(x>0)) /=-1+sinx≤0
故函数为(0,+∞)上的单调减函数,f(x)在(0,+∞)上零点个数不超过一个,
接下来计算:f(0)=
-1>0,f(2π)=-
-1<0
取中点处函数值:f(π)=1-
<0
再取中点处函数值:f(
) =0,找到了这个零点
以上过程将区间[0,2π]二分了二次
故选B
f /(x)= (
| π |
| 2 |
故函数为(0,+∞)上的单调减函数,f(x)在(0,+∞)上零点个数不超过一个,
接下来计算:f(0)=
| π |
| 2 |
| 3π |
| 2 |
取中点处函数值:f(π)=1-
| π |
| 2 |
再取中点处函数值:f(
| π |
| 2 |
以上过程将区间[0,2π]二分了二次
故选B
点评:本题考查了利用零点存在性定理判断函数零点位置,属于基础题.利用导数工具找出此函数的单调性再圆心判断,是解决本题的关键.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
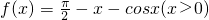 在区间[0,2π]内的零点,二分区间[0,2π]的次数为
在区间[0,2π]内的零点,二分区间[0,2π]的次数为 在区间[0,2π]内的零点,二分区间[0,2π]的次数为( )
在区间[0,2π]内的零点,二分区间[0,2π]的次数为( )