题目内容
己知抛物线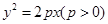 的焦点F恰好是双曲线
的焦点F恰好是双曲线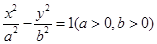 的右焦点,且两条曲线的交点的连线过点F,则该双曲线的离心率为( )
的右焦点,且两条曲线的交点的连线过点F,则该双曲线的离心率为( )
A.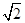 +1 +1 | B.2 | C.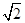 | D.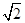 -1 -1 |
A
解析试题分析:
由题意得抛物线上的点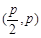 在双曲线上,而
在双曲线上,而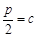 ,所以点
,所以点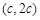 在双曲线上,因此
在双曲线上,因此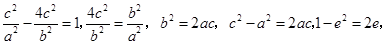 又因为
又因为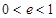 ,所以
,所以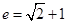 .
.
考点:抛物线通径的应用

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
过抛物线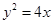 焦点
焦点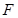 的直线交其于
的直线交其于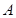 ,
,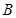 两点,
两点,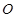 为坐标原点.若
为坐标原点.若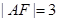 ,则
,则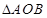 的面积为( )
的面积为( )
A.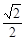 | B.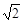 | C.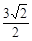 | D.2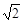 |
双曲线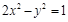 的离心率为( )
的离心率为( )
A.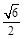 | B.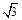 | C.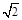 | D. |
已知点F( ,0),直线l:x=-
,0),直线l:x=- ,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M的轨迹是( )
,点B是l上的动点,若过B垂直于y轴的直线与线段BF的垂直平分线交于点M,则点M的轨迹是( )
| A.双曲线 | B.椭圆 |
| C.圆 | D.抛物线 |
已知M是y= x2上一点,F为抛物线的焦点.A在C:(x-1)2+(y-4)2=1上,则|MA|+|MF|的最小值为( )
x2上一点,F为抛物线的焦点.A在C:(x-1)2+(y-4)2=1上,则|MA|+|MF|的最小值为( )
| A.2 | B.4 | C.8 | D.10 |
双曲线 -
- =1(a>0,b>0)的离心率为2,则
=1(a>0,b>0)的离心率为2,则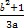 的最小值为( )
的最小值为( )
A.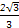 | B.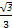 | C.2 | D.1 |
已知椭圆C: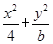 =1,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
=1,直线l:y=mx+1,若对任意的m∈R,直线l与椭圆C恒有公共点,则实数b的取值范围是( )
| A.[1,4) | B.[1,+∞) | C.[1,4)∪(4,+∞) | D.(4,+∞) |
双曲线x2-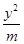 =1的离心率大于
=1的离心率大于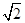 的充分必要条件是( )
的充分必要条件是( )
A.m>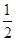 | B.m≥1 |
| C.m>1 | D.m>2 |


