题目内容
已知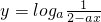 在[0,1]上是x的增函数,则a的取值范围是
在[0,1]上是x的增函数,则a的取值范围是
- A.(0,1)
- B.(1,2)
- C.(0,2)
- D.(2,+∞)
B
分析:由a>0且a≠1,知t=2-ax在[0,1]上是减函数,即s=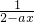 是增函数,从而知y=logas是增函数,再结合函数的定义域,即可求得a的取值范围.
是增函数,从而知y=logas是增函数,再结合函数的定义域,即可求得a的取值范围.
解答:∵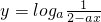 在[0,1]上是x的增函数,函数定义域为∴当0<a<1时,有t=2-ax在[0,1]上是减函数,s=
在[0,1]上是x的增函数,函数定义域为∴当0<a<1时,有t=2-ax在[0,1]上是减函数,s=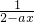 是[0,1]上的增函数,又y=logas是减函数,
是[0,1]上的增函数,又y=logas是减函数,
∴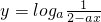 是减函数,不满足题意;
是减函数,不满足题意;
当a>1时,有t=2-ax在[0,1]上是减函数,s=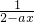 是[0,1]上的增函数,又y=logas在[0,1]上是增函数,
是[0,1]上的增函数,又y=logas在[0,1]上是增函数,
∴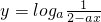 是增函数,满足题意;又
是增函数,满足题意;又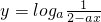 在[0,1]上有意义,∴2-a>0,∴a<2,即1<a<2;
在[0,1]上有意义,∴2-a>0,∴a<2,即1<a<2;
所以a的取值范围是:(1,2);
故选:B.
点评:本题考查了复合函数的单调性问题,是比较容易出错的基础题目.
分析:由a>0且a≠1,知t=2-ax在[0,1]上是减函数,即s=
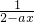 是增函数,从而知y=logas是增函数,再结合函数的定义域,即可求得a的取值范围.
是增函数,从而知y=logas是增函数,再结合函数的定义域,即可求得a的取值范围.解答:∵
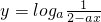 在[0,1]上是x的增函数,函数定义域为∴当0<a<1时,有t=2-ax在[0,1]上是减函数,s=
在[0,1]上是x的增函数,函数定义域为∴当0<a<1时,有t=2-ax在[0,1]上是减函数,s=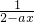 是[0,1]上的增函数,又y=logas是减函数,
是[0,1]上的增函数,又y=logas是减函数,∴
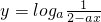 是减函数,不满足题意;
是减函数,不满足题意;当a>1时,有t=2-ax在[0,1]上是减函数,s=
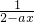 是[0,1]上的增函数,又y=logas在[0,1]上是增函数,
是[0,1]上的增函数,又y=logas在[0,1]上是增函数,∴
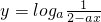 是增函数,满足题意;又
是增函数,满足题意;又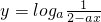 在[0,1]上有意义,∴2-a>0,∴a<2,即1<a<2;
在[0,1]上有意义,∴2-a>0,∴a<2,即1<a<2;所以a的取值范围是:(1,2);
故选:B.
点评:本题考查了复合函数的单调性问题,是比较容易出错的基础题目.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
已知
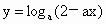 在[0,1]上是x的减函数,则a的取值范围是
在[0,1]上是x的减函数,则a的取值范围是
[
]|
A .(0,1) |
B .(1,2) |
|
C .(0,2) |
D .[2,+∞) |
已知
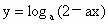 在[0,1]上是关于x的减函数,则a的取值范围是
在[0,1]上是关于x的减函数,则a的取值范围是
[
]|
A .(0,1) |
B .(1,2) |
|
C .(0,2) |
D .[2,+∞) |
已知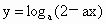 在[0,1]上是x的减函数,则a的取值范围是
在[0,1]上是x的减函数,则a的取值范围是
[ ]
|
A.(0,1) |
B.(1,2) |
|
C.(0,2) |
D.[2,+∞) |
已知
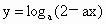 在[0,1]上是减函数,则a的取值范围是
在[0,1]上是减函数,则a的取值范围是
[
]|
A .(0,1) |
B .(1,2) |
|
C .(0,2) |
D .[2,+∞) |
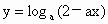 在[0,1]上是关于x的减函数,则a的取值范围是
在[0,1]上是关于x的减函数,则a的取值范围是