题目内容
9.己知函数f(x)=$\left\{\begin{array}{l}{{e}^{x}-a,x≤0}\\{x-\frac{1}{x},x>0}\end{array}\right.$,若关于x的方程f(f(x))=0有且只有一个实数解,则实数a的取值范围为(-∞,-1)∪(-1,+∞).分析 根据题意,分析可得如果f(f(x))=0有且只有一个实数解,则f(x)=1和f(x)=lna(a>0)中只能有1个方程有解,且只有1解,即函数f(x)的图象与y=1或y=lna(a>0)的图象有且只能有一个交点,进而作出函数g(x)=$\left\{\begin{array}{l}{{e}^{x}\\,\\ x≤0}\\{x-\frac{1}{x}\\ \\,\\ x>0}\end{array}\right.$的图象,分析其图象与函数f(x)的图象的位置关系,即可得答案.
解答 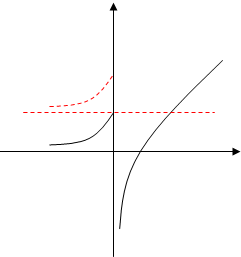 解:根据题意,假设f(t)=0,
解:根据题意,假设f(t)=0,
则当t≤0时,有et-a=0,则t=lna,(a>0)
当t>0时,有t-$\frac{1}{t}$=1,解可得t=1,
如果f(f(x))=0有且只有一个实数解,则f(x)=1和f(x)=lna(a>0)中只能有1个方程有解,且只有1解,
即函数f(x)的图象与y=1或y=lna(a>0)的图象有且只能有一个交点,
作出函数g(x)=$\left\{\begin{array}{l}{{e}^{x}\\,\\ x≤0}\\{x-\frac{1}{x}\\ \\,\\ x>0}\end{array}\right.$的图象,将其图象x≤0的部分向上或向下平移|a|个单位可得函数f(x)的图象,
分析可得,函数f(x)的图象只可能与y=1有且只有一个交点,
且a的取值范围是(-∞,-1]∪(1,+∞);
故答案为:(-∞,-1]∪(1,+∞).
点评 本题考查分段函数的运用,主要考查函数的零点和方程的根的关系,运用分类讨论的思想和函数的值域是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.2015年6月20日是我们的传统节日--”端午节”,这天小明的妈妈为小明煮了5个粽子,其中两个腊肉馅三个豆沙馅,小明随机取出两个,事件A=“取到的两个为同一种馅”,事件B=“取到的两个都是豆沙馅”,则P(B|A)=( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{10}$ | D. | $\frac{3}{10}$ |
4.△ABC中,角A、B、C所对应的边分别a、b、c,已知bcosC+ccosB=2b,则$\frac{a}{2b}$=( )
| A. | 2 | B. | $\frac{1}{2}$ | C. | $\sqrt{2}$ | D. | 1 |
18.若运行所给程序输出的值是16,则输入的实数x值为( )


| A. | 32 | B. | 8 | C. | -4或8 | D. | 4或-4或8 |
19.某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温x(°C)与该小卖部的这种饮料销量y(杯),得到如下数据:
(1)若先从这五组数据中抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(3)根据(Ⅱ)中所得的线性回归方程,若天气预报1月16日的白天平均气温7(°C),请预测该奶茶店这种饮料的销量.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.)
| 日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
| 平均气温x(°C) | 9 | 10 | 12 | 11 | 8 |
| 销量y(杯) | 23 | 25 | 30 | 26 | 21 |
(2)请根据所给五组数据,求出y关于x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(3)根据(Ⅱ)中所得的线性回归方程,若天气预报1月16日的白天平均气温7(°C),请预测该奶茶店这种饮料的销量.
(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$.)
 如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,|AB|=4,有一曲线C过Q点,有一动点P在曲线C上运动且保持|PA|+|PB|的值不变.
如图,ADB为半圆,AB为半圆直径,O为半圆圆心,且OD⊥AB,Q为线段OD的中点,|AB|=4,有一曲线C过Q点,有一动点P在曲线C上运动且保持|PA|+|PB|的值不变. 如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.
如图,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D1D=$\sqrt{2}$,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD中点.