题目内容
已知,椭圆C以双曲线x2-| y2 | 3 |
(1)求椭圆C的方程;
(2)若直线l:y=kx+m与椭圆C相交于M、N两点(M、N不是左右顶点),且以线段MN为直径的圆过点A(2,0),求证:直线l过定点,并求出该定点的坐标.
分析:(1)先由双曲线求出相应的实半轴,虚半轴和半焦距,再利用椭圆和双曲线的关系求解.
(2)由以线段MN为直径的圆过点A(2,0),则线段MN对应的圆周角为直角,有
•
=0,再由M,N是直线与椭圆的交点求解.
(2)由以线段MN为直径的圆过点A(2,0),则线段MN对应的圆周角为直角,有
| AM |
| AN |
解答:解:根据题意:双曲线x2-
=1的焦点坐标为(-2,0),(2,0),顶点坐标为(-1,0),(1,0)
∵椭圆C以双曲线x2-
=1的焦点为顶点,以双曲线的顶点为焦点.
∴椭圆的顶点为(-2,0),(2,0),焦点坐标为2,(-1,0),(1,0)
∴a=2,b=3
∴椭圆的方程是:
+
=1
(2)设A(x1,y1),B(x2,y2) 联立y=kx+m,
+
=1
整理得:(3+4k2)x2+8mkx+4m2-12=0
△=64m2k2-4(4k2+3)(4m2-12)>0
解得:m2<4k2+3 ①
由韦达定理:x1+x2=-8mk/(3+4k2).x1x2=(4m2-12)/(3+4k2)
所以y1y2=k2x1x2+mk(x1+x2)+m2=(3m2-12k2)/(3+4k2)
因为以MV为直径的圆过椭圆C的右顶点A(2,0)
所以
•
=0
∴7m2+16mk+4k2=0
解得:m1=-2k/7,m2=-2k
经检验,当m=-2k/7或m=-2k时,①式均成立
而当m=-2k时,直线l:y=k(x-2),过右顶点,不合题意所以m=-2k/7,
∴直线l:y=k(x-2/7).过定点(2/7,0)
| y2 |
| 3 |
∵椭圆C以双曲线x2-
| y2 |
| 3 |
∴椭圆的顶点为(-2,0),(2,0),焦点坐标为2,(-1,0),(1,0)
∴a=2,b=3
∴椭圆的方程是:
| x2 |
| 4 |
| y2 |
| 3 |
(2)设A(x1,y1),B(x2,y2) 联立y=kx+m,
| x2 |
| 4 |
| y2 |
| 3 |
整理得:(3+4k2)x2+8mkx+4m2-12=0
△=64m2k2-4(4k2+3)(4m2-12)>0
解得:m2<4k2+3 ①
由韦达定理:x1+x2=-8mk/(3+4k2).x1x2=(4m2-12)/(3+4k2)
所以y1y2=k2x1x2+mk(x1+x2)+m2=(3m2-12k2)/(3+4k2)
因为以MV为直径的圆过椭圆C的右顶点A(2,0)
所以
| AM |
| AN |
∴7m2+16mk+4k2=0
解得:m1=-2k/7,m2=-2k
经检验,当m=-2k/7或m=-2k时,①式均成立
而当m=-2k时,直线l:y=k(x-2),过右顶点,不合题意所以m=-2k/7,
∴直线l:y=k(x-2/7).过定点(2/7,0)
点评:本题主要考查圆锥曲线间的关系及性质的应用,同时考查直线与椭圆的位置关系在解决平面图形中的应用.

练习册系列答案
相关题目
 的焦点为顶点,以双曲线的顶点为焦点.
的焦点为顶点,以双曲线的顶点为焦点.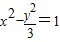 的焦点为顶点,以双曲线的顶点为焦点.
的焦点为顶点,以双曲线的顶点为焦点.