题目内容
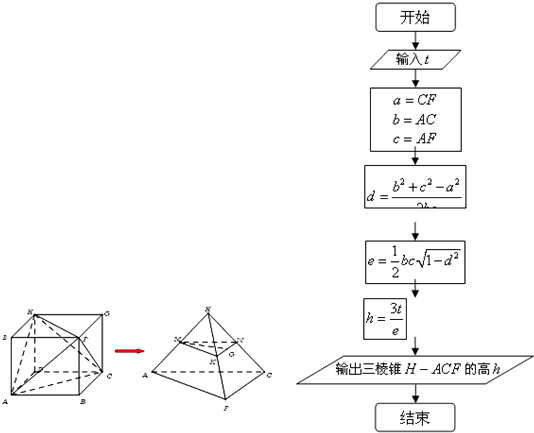
某工厂欲加工一件艺术品,需要用到三棱锥形状的坯材,工人将如图所示的长方体ABCD-EFGH材料切割成三棱锥H-ACF.
(Ⅰ)若点M,N,K分别是棱HA,HC,HF的中点,点G是NK上的任意一点,求证:MG∥平面ACF;
(Ⅱ)已知原长方体材料中,AB=2m,AD=3m,DH=1m,根据艺术品加工需要,工程师必须求出该三棱锥的高.
(i) 甲工程师先求出AH所在直线与平面ACF所成的角θ,再根据公式h=AH•sinθ求出三棱锥H-ACF的高.请你根据甲工程师的思路,求该三棱锥的高.
(ii)乙工程师设计了一个求三棱锥的高度的程序,其框图如图所示,则运行该程序时乙工程师应输入的t的值是多少?(请直接写出t的值,不要求写出演算或推证的过程).
【答案】分析:(Ⅰ)证法一:利用线面平行的判定证明MK∥平面ACF,MN∥平面ACF,从而可得平面MNK∥平面ACF,利用面面平行的性质可得MG∥平面ACF;证法二:利用线面平行的判定证明MG∥平面ACF;
(Ⅱ)(i)建立空间直角坐标系,求出平面ACF的一个法向量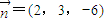 ,求出AH所在直线与平面ACF所成的角θ,再根据公式h=AH•sinθ求出三棱锥H-ACF的高
,求出AH所在直线与平面ACF所成的角θ,再根据公式h=AH•sinθ求出三棱锥H-ACF的高
(ii)t=2.
解答: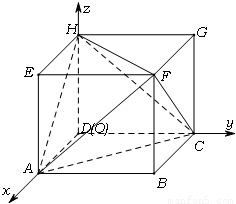 (Ⅰ)证法一:∵HM=MA,HN=NC,HK=KF,
(Ⅰ)证法一:∵HM=MA,HN=NC,HK=KF,
∴MK∥AF,MN∥AC.∵MK?平面ACF,AF?平面ACF,
∴MK∥平面ACF,
同理可证MN∥平面ACF,…(3分)
∵MN,MK?平面MNK,且MK∩MN=M,
∴平面MNK∥平面ACF,…(4分)
又MG?平面MNK,故MG∥平面ACF.…(5分)
证法二:连HG并延长交FC于T,连接AT.
∵HN=NC,HK=KF,
∴KN∥FC,则HG=GT,
又∵HM=MA,∴MG∥AT,…(2分)∵MG?平面ACF,AT?平面ACF,
∴MG∥平面ACF.…(5分)
(Ⅱ)解:(i)如图,分别以DA,DC,DH所在直线为x轴,y轴,z轴建立空间直角坐标系O-xyz.则有A(3,0,0),C(0,2,0),F(3,2,1),H(0,0,1).…(6分)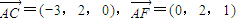 ,
,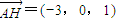 .
.
设平面ACF的一个法向量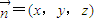 ,
,
则有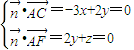 ,解得
,解得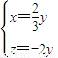 ,
,
令y=3,则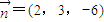 ,…(8分)
,…(8分)
∴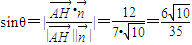 ,…(9分)
,…(9分)
∴三棱锥H-ACF的高为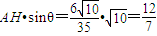 .…(10分)
.…(10分)
(ii)t=2.…(13分)
点评:本小题主要考查直线与直线、直线与平面、平面与平面的位置关系和算法初步等基础知识,考查空间想象能力、推理论证能力及运算求解能力,考查化归与转化思想、数形结合思想、函数与方程思想及应用意识.
(Ⅱ)(i)建立空间直角坐标系,求出平面ACF的一个法向量
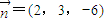 ,求出AH所在直线与平面ACF所成的角θ,再根据公式h=AH•sinθ求出三棱锥H-ACF的高
,求出AH所在直线与平面ACF所成的角θ,再根据公式h=AH•sinθ求出三棱锥H-ACF的高(ii)t=2.
解答:
 (Ⅰ)证法一:∵HM=MA,HN=NC,HK=KF,
(Ⅰ)证法一:∵HM=MA,HN=NC,HK=KF,∴MK∥AF,MN∥AC.∵MK?平面ACF,AF?平面ACF,
∴MK∥平面ACF,
同理可证MN∥平面ACF,…(3分)
∵MN,MK?平面MNK,且MK∩MN=M,
∴平面MNK∥平面ACF,…(4分)
又MG?平面MNK,故MG∥平面ACF.…(5分)
证法二:连HG并延长交FC于T,连接AT.
∵HN=NC,HK=KF,
∴KN∥FC,则HG=GT,
又∵HM=MA,∴MG∥AT,…(2分)∵MG?平面ACF,AT?平面ACF,
∴MG∥平面ACF.…(5分)
(Ⅱ)解:(i)如图,分别以DA,DC,DH所在直线为x轴,y轴,z轴建立空间直角坐标系O-xyz.则有A(3,0,0),C(0,2,0),F(3,2,1),H(0,0,1).…(6分)
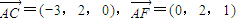 ,
,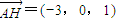 .
.设平面ACF的一个法向量
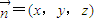 ,
,则有
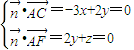 ,解得
,解得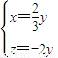 ,
,令y=3,则
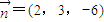 ,…(8分)
,…(8分)∴
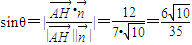 ,…(9分)
,…(9分)∴三棱锥H-ACF的高为
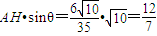 .…(10分)
.…(10分)(ii)t=2.…(13分)
点评:本小题主要考查直线与直线、直线与平面、平面与平面的位置关系和算法初步等基础知识,考查空间想象能力、推理论证能力及运算求解能力,考查化归与转化思想、数形结合思想、函数与方程思想及应用意识.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目