题目内容

解: (1)由已知得=bcsinA=bsin60°,∴b=1.
(1)由已知得=bcsinA=bsin60°,∴b=1.
由余弦定理a2=b2+c2-2bccosA=3,∴a=.
 (2)由正弦定理得2RsinA=a,2RsinB=
(2)由正弦定理得2RsinA=a,2RsinB= b,
b,
∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,
又A,B为三角形内角,∴A+B=90°或A=B.
故△ABC为直角三角形或等腰三角形.
 (1)由已知得=bcsinA=bsin60°,∴b=1.
(1)由已知得=bcsinA=bsin60°,∴b=1.由余弦定理a2=b2+c2-2bccosA=3,∴a=.
 (2)由正弦定理得2RsinA=a,2RsinB=
(2)由正弦定理得2RsinA=a,2RsinB= b,
b,∴2RsinAcosA=2RsinBcosB,即sin2A=sin2B,
又A,B为三角形内角,∴A+B=90°或A=B.
故△ABC为直角三角形或等腰三角形.
略

练习册系列答案
相关题目
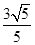
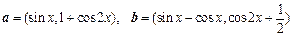 ,定义函数
,定义函数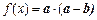
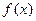 最小正周期;
最小正周期;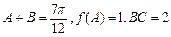 ,求边AC的长.
,求边AC的长.  ( )
( )



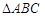 中,
中, 则
则 等于
等于



 中,已知
中,已知 ,则
,则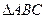 中,已知
中,已知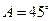 ,
,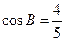 .
. (Ⅰ)求
(Ⅰ)求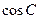 的值;
的值;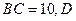 为
为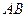 的中点,求
的中点,求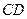 的长.
的长.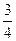 ,则一个底角的余弦值为 .
,则一个底角的余弦值为 .