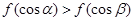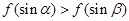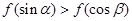题目内容
若不等式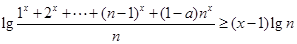 对任意不大于1的实数x和大于1的正整数n都成立,则实数a的取值范围是( )
对任意不大于1的实数x和大于1的正整数n都成立,则实数a的取值范围是( )
A. | B.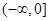 | C.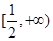 | D.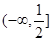 |
D
解析试题分析:由
得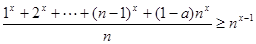 ,即
,即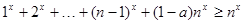
即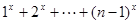

∴ ,令
,令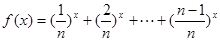 由于
由于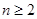 ,故
,故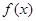 在
在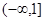 上为减函数,故
上为减函数,故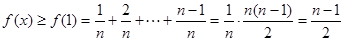
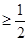 ,∴
,∴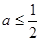 即可,
即可,
故选 .
.
考点:对数式的运算、恒成立问题、函数单调性.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
对任意实数 ,
,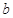 定义运算“⊙”:
定义运算“⊙”: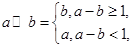 设
设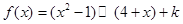 ,若函数
,若函数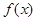 的图象与
的图象与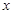 轴恰有三个交点,则
轴恰有三个交点,则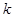 的取值范围是( )
的取值范围是( )
A.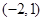 | B.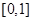 |
C.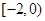 | D.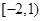 |
函数 的定义域为
的定义域为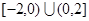 ,其图像上任一点
,其图像上任一点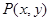 都位于椭圆
都位于椭圆 :
: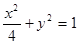 上,下列判断①函数
上,下列判断①函数 一定是偶函数;②函数
一定是偶函数;②函数 可能既不是偶函数,也不是奇函数;③函数
可能既不是偶函数,也不是奇函数;③函数 可能是奇函数;④函数
可能是奇函数;④函数 如果是偶函数,则值域是
如果是偶函数,则值域是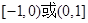 ;⑤函数
;⑤函数 值域是
值域是 ,则一定是奇函数.其中正确的命题个数有( )个
,则一定是奇函数.其中正确的命题个数有( )个
| A.1 | B.2 | C.3 | D.4 |
设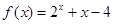 ,则函数
,则函数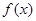 的零点位于区间( )
的零点位于区间( )
| A.(-1,0) | B.(0,1) | C.(1,2) | D.(2,3) |
下列函数中,与函数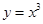 的值域相同的函数为 ( )
的值域相同的函数为 ( )
A.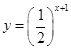 . . | B.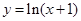 . . | C.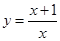 . . | D.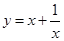 . . |
下列函数是偶函数,且在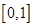 上单调递增的是
上单调递增的是
A. | B.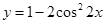 |
C.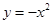 | D.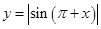 |
已知函数f(x)= 是(-∞,+∞)上的减函数,则a的取值范围是
是(-∞,+∞)上的减函数,则a的取值范围是
( )
| A.(0,3) | B.(0,3] | C.(0,2) | D.(0,2] |
(2013•天津)函数f(x)=2﹣x|log0.5x|﹣1的零点个数为( )
| A.1 | B.2 | C.3 | D.4 |
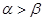 ,则下列结论正确的是( )
,则下列结论正确的是( )