Question

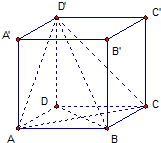如图，在正方形ABCD-A'B'C'D'，
（1）求证：A'B∥平面ACD'；
（2）求证：平面ACD'⊥平面DD'B．

Answer 1

分析：（1）说明四边形A′BCD′为平行四边形．推出A′B∥CD’，然后证明A′B∥平面ACD′．
（2）由四边形ABCD为正方形，证明AC⊥BD，然后证明DD′⊥AC，推出AC⊥平面BDD′，然后证明平面ACD′⊥平面DD′B

解答：证明：（1）∵A′D∥′BC，且A′D=B′C
∴四边形A′BCD′为平行四边形．
∴A′B∥CD′（3分）
又∵A′B?平面ACD′，CD′?平面ACD′
∴A′B∥平面ACD′（6分）
（2）∵四边形ABCD为正方形
∴AC⊥BD                                （8分）
又∵DD′⊥平面ABCD
∴DD′⊥AC                               （10分）
∴AC⊥平面BDD′
而AC?平面ACD′
∴平面ACD′⊥平面DD′B                 （13分）

点评：本题考查直线与平面平行，直线与平面垂直，平面与平面垂直的判断与证明，考查空间想象能力，逻辑推理能力．