题目内容
下列四个命题 ：
(1)随机误差e是衡量预报精确度的一个量，它满足E（e）=0
(2)残差平方和越小的模型，拟合的效果越好；
(3)用相关指数
来刻画回归的效果时，的值越小，说明模型拟合的效果越好；
(4)直线
和各点
的偏差
是该坐标平面上所有直线与这些点的偏差中最小的直线.
其中真命题的个数 （ ）
| A．1 | B．2 | C．3 | D．4 |
C
解析试题分析：由相关系数的定义可知：性相关系数越接近于1，表明两个随机变量线性相关性越强，所以（3）不是真命题，其余命题都是真命题。
考点：本小题主要考查随机误差、相关系数、残差平方和和回归直线等概念的应用.
点评：解决此类问题，关键是搞清楚相关概念，注意适当转化.
练习册系列答案
互动英语系列答案
相关题目
下面是2×2 列联表
| x y | y 1 | y 2 | 合计 |
| x1 | a | 21 | 73 |
| x2 | 2 | 25 | 27 |
| 合计 | b | 46 | 100 |
A．94 、96 B．52 、50 C．52 、54 D．54 、52
在两个变量
与
的回归模型中，分别选择了4个不同模型，它们的相关指数
如下，其中拟和效果最好的模型是（ ）
| A．模型1的相关指数为0.25 | B．模型2的相关指数为0.50 |
| C．模型3的相关指数为0.98 | D．模型4的相关指数为0.80 |
一个容量为35的样本数据，分组后，组距与频数如下：
个；
个；
个；
个；
个；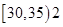
个。则样本在区间
上的频率为
| A．20% | B．69% | C．31% | D．27% |
在某次测量中得到的A样本数据如下：82,84,84,86,86,86,88,88,88,88.若B样本数据 恰好是A样本数据都加2后所得数据，则A，B两样本的下列数字特征对应相同的是
| A．众数 | B．平均数 | C．中位数 | D．标准差 |
随机抽取某中学甲、乙两面个班10名同学，测量他们的身高（单位：cm）后获得身高数据的茎叶图如图甲所示，在这20人中，记身高在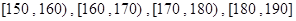
内的人数依次为
，图乙是统计样本中身高在一定范围内的人数的算法流程图，则下列说法正确的是（ ）
| A．由图甲可知甲、乙两班中身高的中位数较大的是甲班，图乙输出的S的值为18 |
| B．由图甲可知甲、乙两班中身高的中位数较大的是乙班，图乙输出的S的值为18 |
| C．由图甲可知甲、乙两班中身高的中位数较大的是乙班，图乙输出的S的值为16 |
| D．由图甲可知甲、乙两班中身高的中位数较大的是甲班，图乙输出的S的值为16 |
在两个变量y与x的回归模型中，分别选择了4个不同模型，它们的
如下，其中拟合效果最好的模型是（ ）
| A．模型1的为0.975 | B．模型2的为0.79 |
| C．模型3的为0.55 | D．模型4的为0.25 |
统计某校1000名学生的数学水平测试成绩，得到样本频率分布直方图如图所示，若满分为100分，规定不低于60分为及格，则及格率是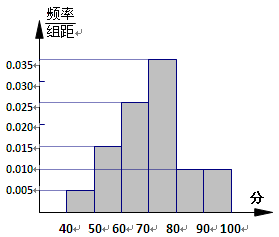
| A．20% |
| B．25% |
| C．6% |
| D．80% |
必过定点（ ）