题目内容
如右图, 是半径为
是半径为 的圆O的两条弦,他们相交于
的圆O的两条弦,他们相交于 的中点
的中点 ,
, =
= ,
, °,则
°,则 =________
=________
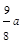
解析试题分析:因为点P是AB的中点,由垂径定理知,OP⊥AB.
在Rt△OPA中,BP=AP=acos30°=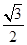 a.
a.
由相交弦定理知,BP•AP=CP•DP,
即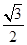 a•
a•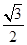 a=CP•
a=CP•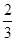 a,所以CP=
a,所以CP=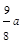 。
。
考点:圆的垂径定理,直角三角形边角关系,相交弦定理。
点评:中档题,平面几何选讲问题,难度一般不大,综合运用三角形、圆的性质加以解决。

练习册系列答案
相关题目
题目内容
如右图, 是半径为
是半径为 的圆O的两条弦,他们相交于
的圆O的两条弦,他们相交于 的中点
的中点 ,
, =
= ,
, °,则
°,则 =________
=________
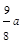
解析试题分析:因为点P是AB的中点,由垂径定理知,OP⊥AB.
在Rt△OPA中,BP=AP=acos30°=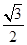 a.
a.
由相交弦定理知,BP•AP=CP•DP,
即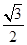 a•
a•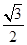 a=CP•
a=CP•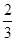 a,所以CP=
a,所以CP=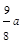 。
。
考点:圆的垂径定理,直角三角形边角关系,相交弦定理。
点评:中档题,平面几何选讲问题,难度一般不大,综合运用三角形、圆的性质加以解决。
