题目内容
解不等式 log
(x2-x-2)>log
2(x-1)
| 1 |
| 2 |
| 1 |
| 2 |
分析:可得 log
(x2-x-2)>log
(2x-2),故有
,解此不等式组求得 不等式的解集.
| 1 |
| 2 |
| 1 |
| 2 |
|
解答:解:由不等式 log
(x2-x-2)>log
2(x-1)可得 log
(x2-x-2)>log
(2x-2),
∴
,即
,解得 2<x<3,
故不等式的解集为 {x|2<x<3}.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
|
|
故不等式的解集为 {x|2<x<3}.
点评:本题主要考查对数不等式的解法,体现了等价转化的数学思想,属于中档题.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
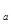 (1-
(1-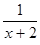 )>0的解集是(-∞,-2),则a的取值范围是( ).
)>0的解集是(-∞,-2),则a的取值范围是( ).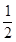 (B).
(B).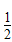 (x2-x-2)>log
(x2-x-2)>log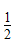 2(x-1)
2(x-1)