题目内容
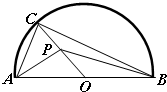如图，半圆的直径AB=4，O为圆心，C为半圆上不同于A、B的任意一点，若P为半径OC上的动点，则(| PA |
| PB |
| PC |
| A、2 | B、0 | C、-1 | D、-2 |
分析：根据O为AB的中点，我们易得(
+
)•
=-2|
|•|
|，又由OPC三点共线，故|
|+|
|=|
|=2为定值，根据基本不等式，我们易得(
+
)•
的最小值．
| PA |
| PB |
| PC |
| PO |
| PC |
| PO |
| PC |
| OC |
| PA |
| PB |
| PC |
解答：解：因为O为AB的中点，
所以
+
=2
，
从而则(
+
)•
=2
•
=-2|
|•|
|；
又|
|+|
|=|
|=2为定值，
所以当且仅当|
|=|
|=1，
即P为OC的中点时，
(
+
)•
取得最小值是-2，
故选D．
所以
| PA |
| PB |
| PO |
从而则(
| PA |
| PB |
| PC |
| PO |
| PC |
| PO |
| PC |
又|
| PO |
| PC |
| OC |
所以当且仅当|
| PO |
| PC |
即P为OC的中点时，
(
| PA |
| PB |
| PC |
故选D．
点评：本题考查的知识点是平面向量的数量积运算，基本不等式，根据O为AB的中点，将(
+
)•
化为-2|
|•|
|，进而转化为一个基本不等式问题是解答本题的关键．
| PA |
| PB |
| PC |
| PO |
| PC |
练习册系列答案
相关题目
（2008•南京二模）如图，半圆的直径AB=2，O为圆心，C为半圆上不同于A，B的任意一点，若P为半径OC上的动点，则
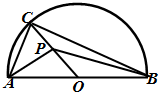如图，半圆的直径AB=6，O为圆心，C为半圆上不同于A、B的任意一点，若P为半径OC上的动点，则(| PA |
| PB |
| PC |
A、
| ||
| B、9 | ||
C、-
| ||
| D、-9 |
如图，半圆的直径AB=4，O为圆心，C是半圆上与A、B不同的任意一点，P是半径OC上的动点，则
如图，半圆的直径AB=2，O为圆心，C是半圆上不同于A，B的任意一点，若P是半径OC上的动点．