题目内容
下列命题中,真命题的序号是 .
①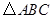 中,
中,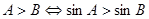
②数列{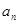 }的前n项和
}的前n项和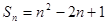 ,则数列{
,则数列{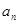 }是等差数列.
}是等差数列.
③锐角三角形的三边长分别为3,4,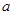 ,则
,则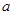 的取值范围是
的取值范围是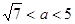 .
.
④等差数列{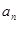 }前n项和为
}前n项和为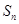 。已知
。已知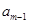 +
+ -
-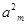 =0,
=0,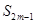 =38,则m=10.
=38,则m=10.
⑤常数数列既是等差数列又是等比数列.
⑥数列{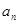 }满足,
}满足,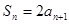 ,则数列{
,则数列{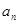 }为等比数列.
}为等比数列.
①③④
解析试题分析:①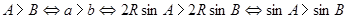 ,所以正确; ②因为
,所以正确; ②因为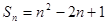 ,所以当
,所以当 时,
时,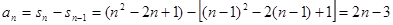 ,又
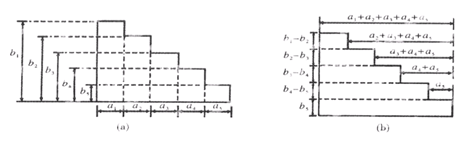
,又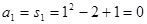 ,不满足上式,所以不是等差数列, 不正确;③因为三角形是锐角三角形,如图所示
,不满足上式,所以不是等差数列, 不正确;③因为三角形是锐角三角形,如图所示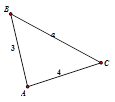
所以有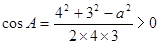 ,
,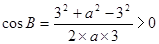 ,
,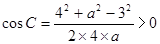 ,解得
,解得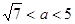 ,正确;④等差数列{
,正确;④等差数列{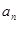 }中,
}中,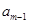 +
+ -
-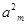 =0,所以由等差中项的知识得:
=0,所以由等差中项的知识得: 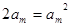 ,解得
,解得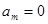 (舍)或
(舍)或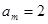 ,又
,又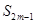 =38,所以
=38,所以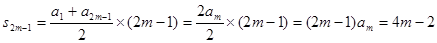 ,所以
,所以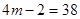 ,所以
,所以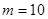 ,正确; ⑤如0,0,0,0,……就不是等比数列,所以不正确; ⑥因为
,正确; ⑤如0,0,0,0,……就不是等比数列,所以不正确; ⑥因为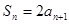 ,所以当
,所以当 时,
时,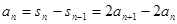 ,所以
,所以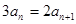 ,所以当
,所以当 时
时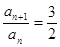 ,又当
,又当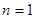 时,
时,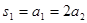 ,所以
,所以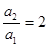 不满足上式,所以不正确.
不满足上式,所以不正确.
考点: 1.正弦定理;2.等差数列的判断;3.余弦定理;4.等差中项;5.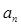 与
与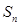 的关系
的关系

练习册系列答案
相关题目
 ,对任意的
,对任意的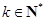 ,当
,当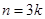 时,
时,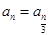 ;当
;当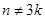 时,
时,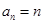 ,那么该数列中的第10个2是该数列的第 项.
,那么该数列中的第10个2是该数列的第 项.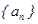 中,
中,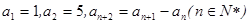 ,则
,则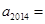 .
. 的前n项和
的前n项和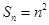 ,则
,则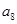 的值为 .
的值为 .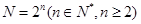 ,将
,将 个数
个数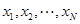 依次放入编号为1,2,…,
依次放入编号为1,2,…,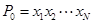 ,将该排列中分别位于奇数与偶数位置的数取出,并按原顺序依次放入对应的前
,将该排列中分别位于奇数与偶数位置的数取出,并按原顺序依次放入对应的前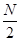 和后
和后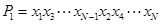 ,将此操作称为
,将此操作称为 变换,将
变换,将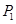 分成两段,每段
分成两段,每段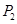 ;当
;当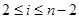 时,将
时,将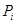 分成
分成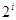 段,每段
段,每段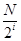 个数,并对每段作
个数,并对每段作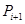 ,例如,当
,例如,当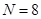 时,
时,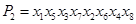 ,此时,
,此时,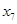 位于
位于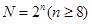 时,
时,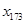 位于
位于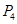 中的第 个位置.
中的第 个位置.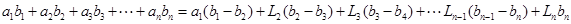
 }的前n项和为
}的前n项和为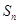 ,且
,且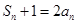 ,则使不等式
,则使不等式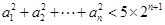 成立的n的最大值为 .
成立的n的最大值为 .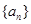 满足
满足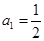 ,
,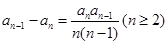 ,则该数列的通项公式
,则该数列的通项公式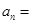
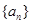 的前
的前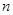 项和
项和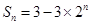 ,则
,则 .
.