题目内容
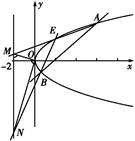
已知E(2,2)是抛物线C:y2=2px上一点,经过点(2,0)的直线l与抛物线C交于A,B两点(不同于点E),直线EA,EB分别交直线x=-2于点M,N.
(1)求抛物线方程及其焦点坐标;
(2)已知O为原点,求证:∠MON为定值.
(1) 抛物线方程为y2=2x,焦点坐标为 (2)见解析
(2)见解析
解析解:(1)∵点E(2,2)在抛物线y2=2px上,
∴4=2p×2,∴p=1.
∴抛物线方程为y2=2x,焦点坐标为 .
.
(2)显然,直线l斜率存在,且不为0.
设l斜率为k,则l方程为y=k(x-2).
由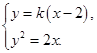
得ky2-2y-4k=0,
设A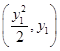 ,B
,B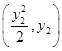 .
.
则y1+y2=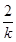 ,y1·y2=-4.
,y1·y2=-4.
∵kEA=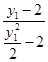 =
=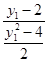 =
=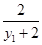 .
.
∴EA方程为y-2=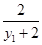 (x-2).
(x-2).
令x=-2,得y=2-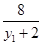 =
=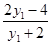 .
.
∴M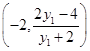 .
.
同理可求得N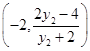 .
.
∴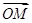 ·
·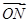 =
=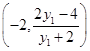 ·
·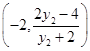
=4+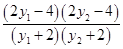
=4+
=0
∴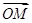 ⊥
⊥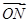 .
.
即∠MON=90°,
∴∠MON为定值.

练习册系列答案
相关题目
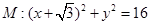 ,动圆
,动圆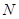 过点
过点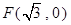 且与圆
且与圆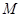 相切,记动圆
相切,记动圆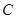 .
.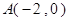 ,过定点
,过定点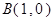 的动直线
的动直线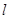 交轨迹
交轨迹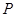 、
、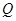 两点,
两点,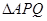 的外心为
的外心为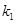 ,直线
,直线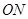 的斜率为
的斜率为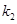 ,求证:
,求证: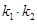 为定值.
为定值. +
+ =1(a>b>0)过点(0,4),离心率为
=1(a>b>0)过点(0,4),离心率为 .
. 的直线被C所截线段的中点坐标.
的直线被C所截线段的中点坐标. 的左顶点
的左顶点 作斜率为2的直线,与椭圆的另一个交点为
作斜率为2的直线,与椭圆的另一个交点为 ,与
,与 轴的交点为
轴的交点为 ,已知
,已知 .
. 与椭圆有且只有一个公共点
与椭圆有且只有一个公共点 ,且与直线
,且与直线 相交于点
相交于点 ,若
,若 轴上存在一定点
轴上存在一定点 ,使得
,使得 ,求椭圆的方程.
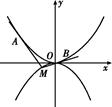
,求椭圆的方程. 时,切线MA的斜率为-
时,切线MA的斜率为- .
.
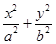 =1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.
=1(a>b>0)的左、右焦点,A是椭圆C的顶点,B是直线AF2与椭圆C的另一个交点,∠F1AF2=60°.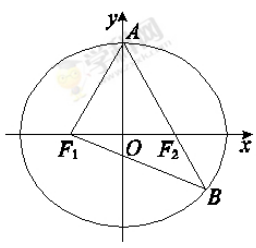
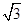 ,求a,b的值.
,求a,b的值. +
+ =1(a>b>0)的左、右顶点分别为A,B,点P是双曲线C2:
=1(a>b>0)的左、右顶点分别为A,B,点P是双曲线C2: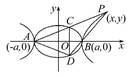
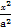 +
+ =1(a>b>0).
=1(a>b>0). ,求椭圆的标准方程.
,求椭圆的标准方程. .
. =2
=2 ,求△AOB的面积.
,求△AOB的面积.