题目内容
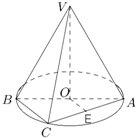如图，AB是圆O的直径，点C是圆O上不同于A，B的一点，点V是圆O所在平面外一点．（Ⅰ） 若点E是AC的中点，求证：OE∥平面VBC；
（Ⅱ） 若VA=VB=VC，求证：VO⊥平面ABC．
分析：（Ⅰ）要证OE∥平面VBC，只需证OE平行于平面VBC内的一条直线即可；
（Ⅱ）要证VO⊥平面ABC，只需证VO垂直于平面ABC内的两条相交直线即可．
（Ⅱ）要证VO⊥平面ABC，只需证VO垂直于平面ABC内的两条相交直线即可．
解答：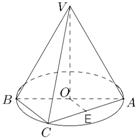
证明：（Ⅰ）∵O，E分别是AB和AC的中点，
∴OE∥BC，
又∵OE?面VBC，BC?面VBC，
∴OE∥面VBC；
（Ⅱ）∵VA=VB，∵△ABC为等腰三角形，
又∵O为AB中点，∴VO⊥AB，
连接OC，在△VOA和△VOC中，OA=OC，VO=VO，VA=VC，
△VOA≌△VOC，
∴∠V0A=∠VOC=90°．∴VO⊥OC，
∵AB∩OC=O，AB?平面ABC，OC?平面ABC，
∴VO⊥平面ABC．
证明：（Ⅰ）∵O，E分别是AB和AC的中点，∴OE∥BC，
又∵OE?面VBC，BC?面VBC，
∴OE∥面VBC；
（Ⅱ）∵VA=VB，∵△ABC为等腰三角形，
又∵O为AB中点，∴VO⊥AB，
连接OC，在△VOA和△VOC中，OA=OC，VO=VO，VA=VC，
△VOA≌△VOC，
∴∠V0A=∠VOC=90°．∴VO⊥OC，
∵AB∩OC=O，AB?平面ABC，OC?平面ABC，
∴VO⊥平面ABC．
点评：本题考查线面平行，线面垂直的判断定理，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，直三棱柱的一个底面ABC内接于圆O，AB是圆O的直径．
与直线
的夹角大小为
B．（不等式选讲）要使关于x的不等式
在实数