题目内容
(2011•温州一模)将一颗骰子投掷两次分别得到点数a,b,则直线ax-by=0与圆(x-2)2+y2=2相交的概率为
.
| 11 |
| 36 |
| 11 |
| 36 |
分析:利用古典概型概率计算公式,先计算总的基本事件数N,再计算事件直线ax-by=0与圆(x-2)2+y2=2相交时包含的基本事件数n,最后事件发生的概率为P=
| n |
| N |
解答:解:∵直线ax-by=0与圆(x-2)2+y2=2相交,∴圆心到直线的距离
<
即a<b
∵设一颗骰子投掷两次分别得到点数为(a,b),则这样的有序整数对共有6×6=36个
其中a<b的有(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共5+4+3+2+1=15个,
又由(1,2)(2,4)(3,6)算同一条直线
(1,3)(2,6)算同一条直线
(2,3)(4,6)算同一条直线
则共有11条直线;
∴直线ax-by=0与圆(x-2)2+y2=2相交的概率为P=
故答案为
.
| |2a| | ||
|
| 2 |
即a<b
∵设一颗骰子投掷两次分别得到点数为(a,b),则这样的有序整数对共有6×6=36个
其中a<b的有(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),(3,4),(3,5),(3,6),(4,5),(4,6),(5,6)共5+4+3+2+1=15个,
又由(1,2)(2,4)(3,6)算同一条直线
(1,3)(2,6)算同一条直线
(2,3)(4,6)算同一条直线
则共有11条直线;
∴直线ax-by=0与圆(x-2)2+y2=2相交的概率为P=
| 11 |
| 36 |
故答案为
| 11 |
| 36 |
点评:本题考查了古典概型概率的计算方法,乘法计数原理,分类计数原理,直线与圆的位置关系及其判断

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
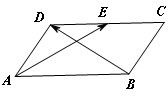 (2011•温州一模)在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,E为CD的中点,则
(2011•温州一模)在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,E为CD的中点,则