题目内容
(2011•温州一模)若集合A={x|x2-2x<0},B={x|y=lg(x-1)},则A∩B为
{x|1<x<2}
{x|1<x<2}
.分析:求出集合A中一元二次不等式的解集确定出集合A,根据负数和0没有对数,得到x-1大于0,求出x的范围确定出集合B,求出两集合的交集即可.
解答:解:由集合A中的不等式x2-2x<0,
因式分解得:x(x-2)<0,
可化为:
或
,解得:0<x<2,
所以集合A={x|0<x<2};
由集合B中的函数y=lg(x-1),得到x-1>0,解得:x>1,
所以集合B={x|x>1},
则A∩B={x|1<x<2}.
故答案为:{x|1<x<2}
因式分解得:x(x-2)<0,
可化为:
|
|
所以集合A={x|0<x<2};
由集合B中的函数y=lg(x-1),得到x-1>0,解得:x>1,
所以集合B={x|x>1},
则A∩B={x|1<x<2}.
故答案为:{x|1<x<2}
点评:本题属于以一元二次不等式的解集和对数函数的定义域为平台,考查了交集的运算,是一道基础题.也是高考中常考的题型.

练习册系列答案
相关题目
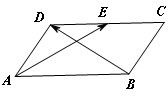 (2011•温州一模)在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,E为CD的中点,则
(2011•温州一模)在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,E为CD的中点,则