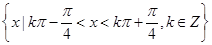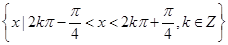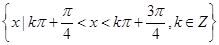题目内容
已知函数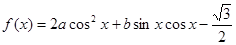 ,且
,且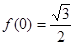 ,
,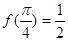 。
。
(1)求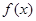 的最小正周期;
的最小正周期;
(2)求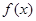 的单调递减区间;
的单调递减区间;
(3)函数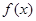 的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
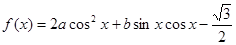 ,且
,且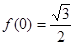 ,
,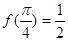 。
。(1)求
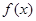 的最小正周期;
的最小正周期;(2)求
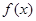 的单调递减区间;
的单调递减区间;(3)函数
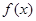 的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?
的图象经过怎样的平移才能使所得图象对应的函数成为奇函数?(1)π (2)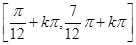 (k∈Z). (3)
(k∈Z). (3)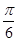
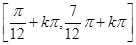 (k∈Z). (3)
(k∈Z). (3)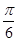
本试题主要考查了三角函数的图像和性质的运用。
解:(1)由f(0)=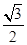 ,得2a-
,得2a-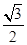 =
=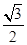 ,∴2a=
,∴2a=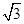 ,则a=
,则a=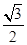 ,
,
由f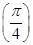 =
=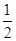 ,得
,得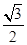 +
+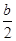 -
-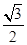 =
=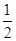 ,∴b=1,∴f(x)=
,∴b=1,∴f(x)=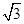 cos2x+sin xcosx-
cos2x+sin xcosx-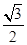
=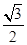 cos 2x+
cos 2x+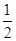 ·sin 2x=sin
·sin 2x=sin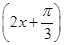 ,∴函数f(x)的最小正周期T=
,∴函数f(x)的最小正周期T=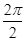 =π.
=π.
(2)由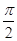 +2kπ≤2x+
+2kπ≤2x+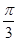 ≤
≤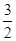 π+2kπ(k∈Z),得
π+2kπ(k∈Z),得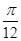 +kπ≤x≤
+kπ≤x≤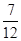 π+kπ(k∈Z),
π+kπ(k∈Z),
∴f(x)的单调递减区间是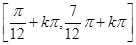 (k∈Z).
(k∈Z).
(3)∵f(x)=sin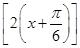 ,∴奇函数y=sin 2x的图象左移
,∴奇函数y=sin 2x的图象左移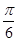 个单位,
个单位,
即得到f(x)的图象, 故函数f(x)的图象右移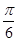 个单位后对应的函数成为奇函数
个单位后对应的函数成为奇函数
解:(1)由f(0)=
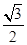 ,得2a-
,得2a-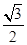 =
=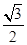 ,∴2a=
,∴2a=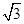 ,则a=
,则a=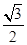 ,
,由f
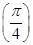 =
=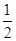 ,得
,得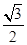 +
+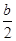 -
-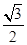 =
=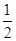 ,∴b=1,∴f(x)=
,∴b=1,∴f(x)=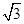 cos2x+sin xcosx-
cos2x+sin xcosx-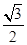
=
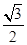 cos 2x+
cos 2x+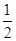 ·sin 2x=sin
·sin 2x=sin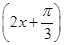 ,∴函数f(x)的最小正周期T=
,∴函数f(x)的最小正周期T=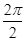 =π.
=π.(2)由
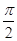 +2kπ≤2x+
+2kπ≤2x+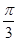 ≤
≤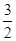 π+2kπ(k∈Z),得
π+2kπ(k∈Z),得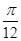 +kπ≤x≤
+kπ≤x≤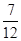 π+kπ(k∈Z),
π+kπ(k∈Z),∴f(x)的单调递减区间是
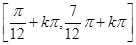 (k∈Z).
(k∈Z).(3)∵f(x)=sin
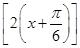 ,∴奇函数y=sin 2x的图象左移
,∴奇函数y=sin 2x的图象左移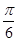 个单位,
个单位, 即得到f(x)的图象, 故函数f(x)的图象右移
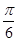 个单位后对应的函数成为奇函数
个单位后对应的函数成为奇函数
练习册系列答案
相关题目
 ,其中
,其中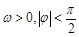 ,若
,若 ,且图象的一条对称轴离一个对称中心的最近距离是
,且图象的一条对称轴离一个对称中心的最近距离是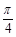 .
.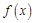 的解析式;
的解析式; 是
是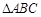 的三个内角,且
的三个内角,且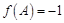 ,求
,求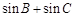 的取值范围
的取值范围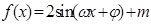 ,对任意实数
,对任意实数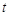 ,都有
,都有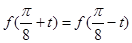 ,且
,且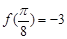 , 则实数
, 则实数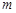 的值等于 .
的值等于 .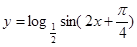 的单调减区间为( )
的单调减区间为( )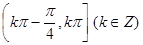
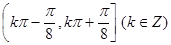
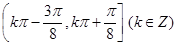
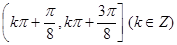
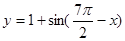 的图像( )A关于x轴对称 B 关于y轴对称 C关于原点对称D 关于直线
的图像( )A关于x轴对称 B 关于y轴对称 C关于原点对称D 关于直线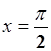 对称
对称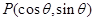 在直线
在直线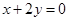 上,则
上,则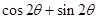 =( )
=( )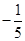
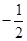
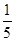
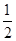
 )的一个增区间是( )
)的一个增区间是( )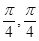 ]
]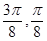 ]
]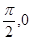 ]
]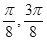 ]
]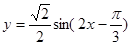 的最大值是( )
的最大值是( )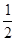
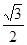
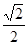
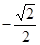
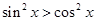 ,则
,则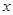 的取值范围是:( )
的取值范围是:( )