题目内容
（2013•徐汇区一模）对于直角坐标平面xOy内的点A（x，y）（不是原点），A的“对偶点”B是指：满足|OA||OB|=1且在射线OA上的那个点．若P，Q，R，S是在同一直线上的四个不同的点（都不是原点），则它们的“对偶点”P′，Q′，R′，S′（ ）
分析：直接利用已知条件|OA||OB|=1，分类讨论：当P，Q，R，S是在过坐标原点的同一直线上的四个不同的点时，则说明它们的“对偶点”P′，Q′，R′，S′都在射线OA上；当P，Q，R，S是在不过坐标原点的同一直线上的四个不同的点时，则说明它们的“对偶点”P′，Q′，R′，S′都在一个圆上，推出结果．
解答：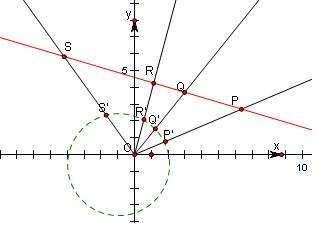
解：因为对于直角坐标平面xOy内的点A（x，y）（不是原点），
①当P，Q，R，S是在过坐标原点的同一直线上的四个不同的点时，
则说明它们的“对偶点”P′，Q′，R′，S′都在射线OA上；故排除选项B、D．
②当P，Q，R，S是在不过坐标原点的同一直线上的四个不同的点时，如图，因为满足：“|OA||OB|=1”，
则说明它们的“对偶点”P′，Q′，R′，S′一定不共线，都在一个圆上，排除选项A．
故选C．
解：因为对于直角坐标平面xOy内的点A（x，y）（不是原点），①当P，Q，R，S是在过坐标原点的同一直线上的四个不同的点时，
则说明它们的“对偶点”P′，Q′，R′，S′都在射线OA上；故排除选项B、D．
②当P，Q，R，S是在不过坐标原点的同一直线上的四个不同的点时，如图，因为满足：“|OA||OB|=1”，
则说明它们的“对偶点”P′，Q′，R′，S′一定不共线，都在一个圆上，排除选项A．
故选C．
点评：本题考查新定义的应用，圆的定义的应用，充分理解题意是解题的关键，就是抓住|OA||OB|=1是关键点．
练习册系列答案
夺冠金卷全能练考系列答案
相关题目