题目内容
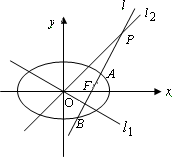
椭圆C的方程
（a＞b＞0），点A、B分别是椭圆长轴的左右端点，左焦点为（-4，0），且过点P
，
（1）求椭圆C的方程；
（2）已知F是椭圆C的右焦点，以AF为直径的圆记为圆M，试问过点P能否引圆M的切线，若能，求出这条切线与x轴及圆M的弦PF所对的劣弧围成图形的面积，若不能，说明理由。
（a＞b＞0），点A、B分别是椭圆长轴的左右端点，左焦点为（-4，0），且过点P，（1）求椭圆C的方程；
（2）已知F是椭圆C的右焦点，以AF为直径的圆记为圆M，试问过点P能否引圆M的切线，若能，求出这条切线与x轴及圆M的弦PF所对的劣弧围成图形的面积，若不能，说明理由。
解：（1）设椭圆的左右焦点为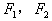
，
∴
，
∴
，
∴
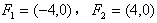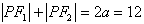，c=4，
∴b2=20，
∴
；
（2）A（-6，0），F2（4，0），
∴圆M：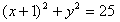
，
又（-1，0）到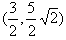
的距离为5，
∴
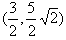是圆M上的点，
∴过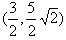
圆M的切线方程为
，
设切线与x轴的交点为C，所求的面积为S，
则S=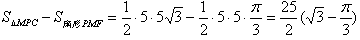
。
，∴
，∴
，∴
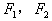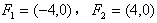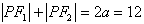，c=4， ∴b2=20，
∴
；（2）A（-6，0），F2（4，0），
∴圆M：
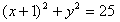，又（-1，0）到
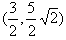的距离为5，∴
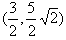是圆M上的点，∴过
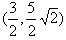圆M的切线方程为，设切线与x轴的交点为C，所求的面积为S，
则S=
。
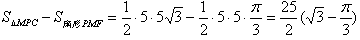练习册系列答案
相关题目
(a＞b＞0)，
、
分别是左右两个焦点，A为右顶点，l为左准线．过
与椭圆相交于P、Q两点，且满足条件
(c为半焦距)．过点P作PT⊥l，T为垂足．
时，求证：
；
时，求实数m的取值范围．
(a＞b＞0)，双曲线
的两条渐近线为l1，l2，过椭圆C的右焦点F作直线l，使l⊥l1，又l与l2交于P点，设l与椭圆C的两个交点由上至下依次为A、B(如图)．
的最大值．
(a＞b＞0)，斜率为1的直线l与椭圆C交于A(x1，y1)，B(x2，y2)两点．
，直线l过点M(b，0)且
，求椭圆的方程；
(λ＞0)，若点P在椭圆C上，求λ的取值范围．
(a＞b＞0),双曲线
的通过第二,第四象限的渐近线为l1,通过第一,第三象限的渐近线为l2.过椭圆C的右焦点F的直线l⊥l1,又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A,B.
|的最大值.