题目内容
14．设点O为△ABC外心，H为其垂心，延长BO交外接圆于点D，则$\overrightarrow{DC}$与$\overrightarrow{AH}$（ ）| A． | 相等 | B． | 仅是模相等 | C． | 不相等 | D． | 共线但不相等 |
分析 根据题意，延长AH交BC于点E，连接CF并延长，交AB于点F，连接AD，证明四边形AHCD是平行四边形，即可得出$\overrightarrow{DC}$=$\overrightarrow{AH}$．
解答 解：延长AH交BC于点E，连接CF并延长，交AB于点F，连接AD，
如图所示：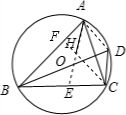
则AE⊥BC，DC⊥BC，
且CF⊥AB，DA⊥AB，
∴AE∥DC，AD∥FC，
∴四边形AHCD是平行四边形，
∴DC∥AH，且DC=AH，
∴$\overrightarrow{DC}$=$\overrightarrow{AH}$．
故选：A．
点评 本题考查了平行与垂直的应用问题，也考查了推理与证明的应用问题，是中档题目．
练习册系列答案
课时训练江苏人民出版社系列答案
相关题目
9．已知数列{an}中的首项a1=1，且满足an+1=$\frac{1}{2}$an+$\frac{1}{2n}$，则此数列的第三项是（ ）
| A． | 1 | B． | $\frac{1}{2}$ | C． | $\frac{3}{4}$ | D． | $\frac{5}{8}$ |
19．如果把函数y=$\frac{1}{4}$sin2x的图象按向量$\overrightarrow{v}$平移，就可以得到函数y=$\frac{1}{4}$sin（2x-$\frac{π}{3}$）的图象，那么向量$\overrightarrow{v}$的坐标是（ ）
| A． | （$\frac{π}{3}$，0） | B． | （$\frac{π}{6}$，0） | C． | （-$\frac{π}{3}$，0） | D． | （-$\frac{π}{6}$，0） |
6．下列四个集合中，是空集的是（ ）
| A． | {0} | B． | {x|x＞8，且x＜5} | C． | {x∈N|x2-1=0} | D． | {x|x＞4} |