题目内容
例4.若正数a,b,c满足a+b+c=1,求证:(a+| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 100 |
| 3 |
分析:首先根据题意设出a,b,c的值,然后分别分析a2+b2+c2,与
+
+
的取值范围,最后化简(a+
)2+(b+
)2+(c+
)2即可求证结论成立.
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
解答:解:∵若正数a,b,c满足a+b+c=1
∴设a=
+x,b=
+y,c=
+z(其中x+y+z=0)
∴a2+b2+c2
=
+2(x+y+z)+x2+y2+z2≥
∵
+
+
≥3×(
)
又∵1=a+b+c≥3(abc)
∴abc≤
∴
+
+
≥3×(
)
≥27
∴(a+
)2+(b+
)2+(c+
)2
=a2+b2+c2+
+
+
+6
≥
+27+6
=
∴(a+
)2+(b+
)2+(c+
)2≥
.
∴设a=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∴a2+b2+c2
=
| 1 |
| 3 |
| 1 |
| 3 |
∵
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
| 1 |
| (abc)2 |
| 1 |
| 3 |
又∵1=a+b+c≥3(abc)
| 1 |
| 3 |
∴abc≤
| 1 |
| 27 |
∴
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
| 1 |
| (abc)2 |
| 1 |
| 3 |
∴(a+
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
=a2+b2+c2+
| 1 |
| a2 |
| 1 |
| b2 |
| 1 |
| c2 |
≥
| 1 |
| 3 |
=
| 100 |
| 3 |
∴(a+
| 1 |
| a |
| 1 |
| b |
| 1 |
| c |
| 100 |
| 3 |
点评:本题考查不等式的证明,通过对需要证明的不等式进行化简,分块进行证明.涉及基本不等式以及不等式的转换,需要对知识熟练掌握并运用,属于基础题.

练习册系列答案
相关题目
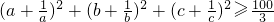 .
.