题目内容
(16分)已知函数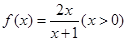
(1)求证:函数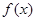 在
在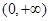 上为单调增函数;
上为单调增函数;
(2)设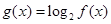 ,求
,求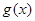 的值域;
的值域;
(3)对于(2)中函数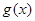 ,若关于
,若关于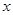 的方程
的方程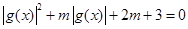 有三个不同的实数解,求
有三个不同的实数解,求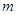 的取值范围.
的取值范围.
(1)求证:函数
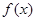 在
在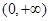 上为单调增函数;
上为单调增函数;(2)设
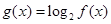 ,求
,求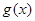 的值域;
的值域; (3)对于(2)中函数
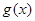 ,若关于
,若关于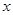 的方程
的方程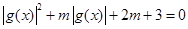 有三个不同的实数解,求
有三个不同的实数解,求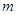 的取值范围.
的取值范围.(1)见解析;(2)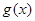 值域为
值域为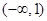 ;(3)
;(3)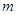 的取值范围为
的取值范围为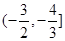 。
。
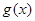 值域为
值域为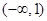 ;(3)
;(3)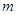 的取值范围为
的取值范围为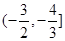 。
。本试题主要是考查了函数的单调性和最值问题,以及函数与方程的思想的综合运用
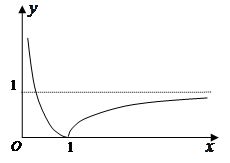
(1)根据已知关系式设出变量,作差,变形定号得到结论。
(2)在第一问的基础上,可知分析函数的单调性得到值域。
((3)因为由(2)可知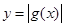 可知其图像,然后徐结合图像,
可知其图像,然后徐结合图像,
设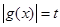 ,则
,则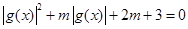 有三个不同的实数解,即为
有三个不同的实数解,即为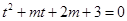 有两个根,且一个在
有两个根,且一个在 上,一个在
上,一个在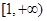 上,然后分析得到m的范围。
上,然后分析得到m的范围。
(1)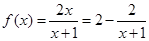 ,设
,设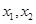 是
是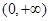 上的任意两个数,且
上的任意两个数,且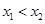 ,……2分
,……2分
则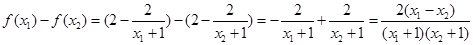 ……4分
……4分
因为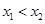 ,∴
,∴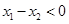 ,∴
,∴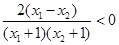 即
即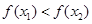
所以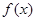 在
在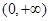 上为增函数, …………………………6分
上为增函数, …………………………6分
(2)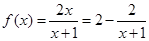 ,
,
因为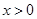 ,所以
,所以 ,所以
,所以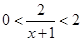 ,
,
即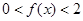 …………………………8分
…………………………8分
又因为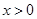 时,
时,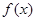 单调递增,
单调递增,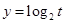 单调递增,
单调递增,
所以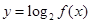 单调递增,所以
单调递增,所以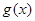 值域为
值域为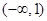 …………………………10分
…………………………10分
(3)由(2)可知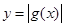 大致图象如右图所示,
大致图象如右图所示,
设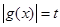 ,则
,则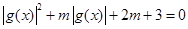 有三个不同的实数解,即为
有三个不同的实数解,即为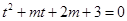 有两个根,且一个在
有两个根,且一个在 上,一个在
上,一个在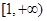 上,设
上,设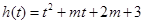 ………12分
………12分
①当有一个根为1时,
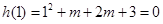 ,
,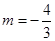 ,此时另一根为
,此时另一根为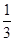 适合题意; ………………13分
适合题意; ………………13分
②当没有根为1时, ,得
,得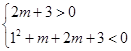 ,∴
,∴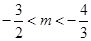
∴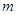 的取值范围为
的取值范围为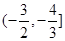 …………………………16分
…………………………16分
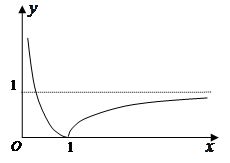
(1)根据已知关系式设出变量,作差,变形定号得到结论。
(2)在第一问的基础上,可知分析函数的单调性得到值域。
((3)因为由(2)可知
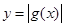 可知其图像,然后徐结合图像,
可知其图像,然后徐结合图像,设
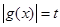 ,则
,则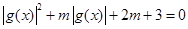 有三个不同的实数解,即为
有三个不同的实数解,即为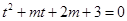 有两个根,且一个在
有两个根,且一个在 上,一个在
上,一个在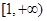 上,然后分析得到m的范围。
上,然后分析得到m的范围。(1)
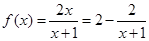 ,设
,设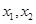 是
是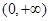 上的任意两个数,且
上的任意两个数,且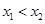 ,……2分
,……2分则
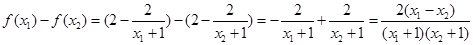 ……4分
……4分因为
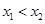 ,∴
,∴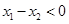 ,∴
,∴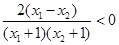 即
即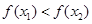
所以
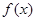 在
在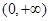 上为增函数, …………………………6分
上为增函数, …………………………6分(2)
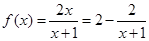 ,
,因为
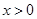 ,所以
,所以 ,所以
,所以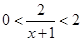 ,
,即
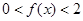 …………………………8分
…………………………8分又因为
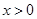 时,
时,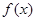 单调递增,
单调递增,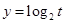 单调递增,
单调递增,所以
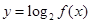 单调递增,所以
单调递增,所以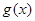 值域为
值域为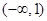 …………………………10分
…………………………10分(3)由(2)可知
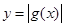 大致图象如右图所示,
大致图象如右图所示,设
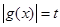 ,则
,则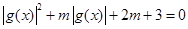 有三个不同的实数解,即为
有三个不同的实数解,即为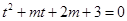 有两个根,且一个在
有两个根,且一个在 上,一个在
上,一个在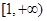 上,设
上,设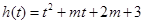 ………12分
………12分①当有一个根为1时,
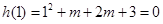 ,
,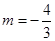 ,此时另一根为
,此时另一根为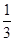 适合题意; ………………13分
适合题意; ………………13分②当没有根为1时,
 ,得
,得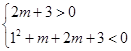 ,∴
,∴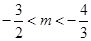
∴
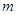 的取值范围为
的取值范围为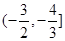 …………………………16分
…………………………16分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
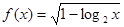 的定义域为 。
的定义域为 。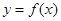 定义域为
定义域为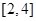 ,则
,则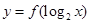 的定义域为( )
的定义域为( )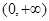
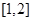
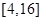
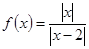 为偶函数; (2)函数
为偶函数; (2)函数 ;
;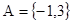 ,
,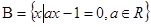 ,若
,若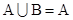 ,则实数
,则实数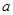 的取值集合为
的取值集合为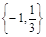 ; (4)集合
; (4)集合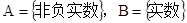 ,对应法则f:“求平方根”,则
,对应法则f:“求平方根”,则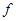 是A到B的映射;你认为正确命题的序号是 (把正确的序号都写上).
是A到B的映射;你认为正确命题的序号是 (把正确的序号都写上).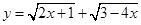 的定义域为( )
的定义域为( )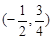
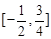
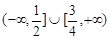
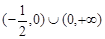
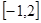 ,求f(2x+1)的定义域.(8分)
,求f(2x+1)的定义域.(8分) 的定义域为( ).
的定义域为( ). 



 的定义域是
的定义域是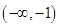



 ,
, 是虚数单位,则
是虚数单位,则 ________.
________.