题目内容
(2013•江门一模)已知函数f(x)=ax2-bx-1,其中a∈(0,2],b∈(0,2],在其取值范围内任取实数a、b,则函数f(x)在区间[1,+∞)上为增函数的概率为( )
分析:由已知中a∈(0,2],b∈(0,2],可求出SΩ,进而根据函数f(x)=ax2-bx-1的图象是开口朝上,且以x=
为对称轴的抛物线,可得函数f(x)在区间[1,+∞)上为增函数时,a∈(0,2],b∈(0,2],b≤2a,进而求出SA,代入几何概型概率公式,可得答案.
| b |
| 2a |
解答:解:∵Ω={(a,b)|a∈(0,2],b∈(0,2]},
∴SΩ=2×2=4
则函数f(x)=ax2-bx-1的图象是开口朝上,且以x=
为对称轴的抛物线,
记“函数f(x)在区间[1,+∞)上为增函数”为事件A
则A={(a,b)|a∈(0,2],b∈(0,2],
≤1}={(a,b)|a∈(0,2],b∈(0,2],b≤2a},
如图所示:
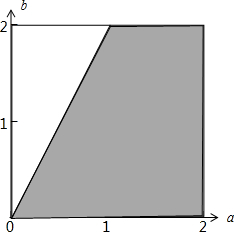
则SA=
(1+2)×2=3
∴P(A)=
=
故函数f(x)在区间[1,+∞)上为增函数的概率为
故选D
∴SΩ=2×2=4
则函数f(x)=ax2-bx-1的图象是开口朝上,且以x=
| b |
| 2a |
记“函数f(x)在区间[1,+∞)上为增函数”为事件A
则A={(a,b)|a∈(0,2],b∈(0,2],
| b |
| 2a |
如图所示:

则SA=
| 1 |
| 2 |
∴P(A)=
| SA |
| SΩ |
| 3 |
| 4 |
故函数f(x)在区间[1,+∞)上为增函数的概率为
| 3 |
| 4 |
故选D
点评:本题考查的知识点是几何概型,几何概型分长度类,面积类,角度类,体积类,解答的关键是根据已知计算出所有基本事件对应的几何量和满足条件的基本事件对应的几何量

练习册系列答案
相关题目