题目内容
设 是三角形的一个内角,
是三角形的一个内角, 且
且 ,则方程
,则方程 表示的曲线是焦点 在 _轴上的__ (填抛物线、椭圆、双曲线的一种)
表示的曲线是焦点 在 _轴上的__ (填抛物线、椭圆、双曲线的一种)
【答案】
y、椭圆
【解析】
试题分析:因为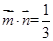 ,所以
,所以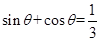 ,两边平方得:
,两边平方得: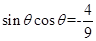 ,因为
,因为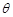 是三角形的一个内角,所以
是三角形的一个内角,所以 ,
,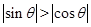 ,所以
,所以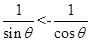 。所以
。所以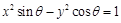 化为:
化为: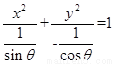 表示焦点在y轴上的椭圆。
表示焦点在y轴上的椭圆。
考点:向量的数量积;圆锥曲线的方程;同角三角函数关系式;三角函数符号的判断。
点评:熟练掌握判断椭圆焦点所在的坐标轴。方程 ,当
,当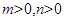 且
且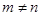 时时表示椭圆;当
时时表示椭圆;当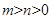 时,表示焦点在x轴上的椭圆;当
时,表示焦点在x轴上的椭圆;当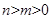 时表示焦点在y轴上的椭圆。
时表示焦点在y轴上的椭圆。

练习册系列答案
 智能训练练测考系列答案
智能训练练测考系列答案
相关题目
设θ是三角形的一个内角,且sinθ+cosθ=
,则方程x2sinθ-y2cosθ=1表示的曲线是( )
| 1 |
| 5 |
| A、焦点在x轴上的双曲线 |
| B、焦点在x轴上的椭圆 |
| C、焦点在y轴上的双曲线 |
| D、焦点在y轴上的椭圆 |
 是三角形的一个内角,且
是三角形的一个内角,且 ,则方程
,则方程 所表示的曲线是( )
所表示的曲线是( ) 轴上的双曲线 B.焦点在
轴上的双曲线 B.焦点在 轴上的双曲线
轴上的双曲线