题目内容
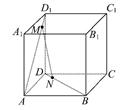
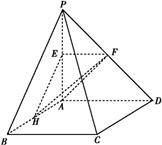
如图,四棱锥 中,
中,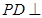 平面
平面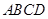 ,底面
,底面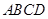 为矩形,
为矩形,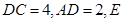 为
为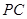 的中点.
的中点.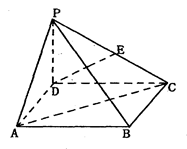
(1)求证: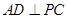 ;
;
(2)在线段 上是否存在一点
上是否存在一点 ,使得
,使得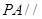 平面
平面 ?若存在,求出
?若存在,求出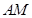 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
(1)证明详见解析;(2)当 为线段
为线段 的中点时,满足
的中点时,满足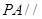 平面
平面 ,此时
,此时 .
.
解析试题分析:(1)要证线线垂直,通常只需证线面垂直,本题中要证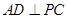 ,只需证明
,只需证明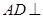 平面
平面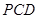 ,而要证
,而要证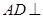 平面
平面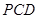 ,又只需证
,又只需证 垂直于平面
垂直于平面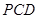 内的两条相交直线
内的两条相交直线 即可,这两个垂直关系,由题中的
即可,这两个垂直关系,由题中的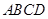 为矩形及
为矩形及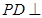 平面
平面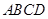 不难得到,命题得证;(2)先假设在线段
不难得到,命题得证;(2)先假设在线段 上能找到一点
上能找到一点 ,使得
,使得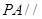 平面
平面 ,此时平面
,此时平面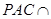 平面
平面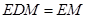 ,
, 平面
平面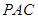 ,由线面平行的性质可知
,由线面平行的性质可知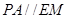 ,由
,由 是
是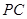 的中点,在
的中点,在 中可知,
中可知, 也是
也是 的中点,此时再根据题中的条件,即可求出
的中点,此时再根据题中的条件,即可求出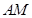 的值,最后采用综合法进行证明即可,问题得以解决.
的值,最后采用综合法进行证明即可,问题得以解决.
试题解析:(1)证明:因为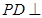 平面
平面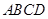 ,
,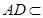 平面
平面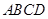 ,所以
,所以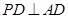
又因为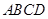 是矩形,所以
是矩形,所以
因为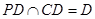 ,所以
,所以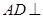 平面
平面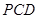 4分
4分
又因为 平面
平面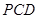 ,所以
,所以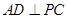 6分
6分
(2)取 中点
中点 ,连结
,连结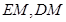
因为 为
为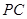 的中点,
的中点, 是
是 的中点,所以
的中点,所以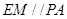
又因为 平面
平面 ,
,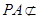 平面
平面 ,所以
,所以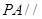 平面
平面 10分
10分
此时
即在 边上存在一点
边上存在一点 ,使得
,使得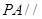 平面
平面 ,
,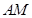 的长为
的长为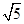 12分.
12分.
考点:1.空间中的垂直关系;2.空间中的平行关系.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
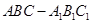 中,
中,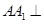 平面
平面 ,
, .以
.以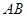 ,
, 为邻边作平行
为邻边作平行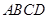 ,连接
,连接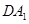 和
和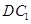 .
. 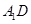
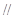 平面
平面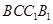 ;
; 平面
平面 .
.
 中,侧面
中,侧面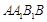 为菱形,且
为菱形,且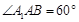 ,
, ,
,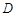 是
是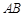 的中点.
的中点.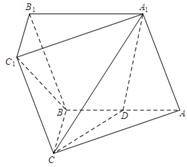
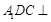 平面
平面 ;
; ∥平面
∥平面 .
.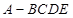 ,
,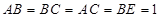 ,
,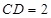 ,
,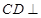 平面
平面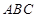 ,
,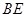 ∥
∥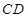 ,
,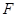 为
为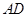 的中点.
的中点.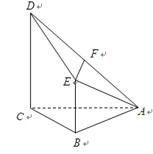
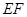 ∥平面
∥平面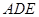
 平面
平面 ;
; ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点
ABCD中,AB⊥AC,AB⊥PA,AB∥CD,AB=2CD,E,F,G,M,N分别为PB,AB,BC,PD,PC的中点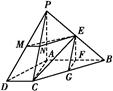
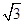 的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2
的菱形,∠BAD=120°,且PA⊥平面ABCD,PA=2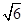 ,M、N分别为PB、PD的中点.
,M、N分别为PB、PD的中点.

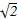 ),连接MN.
),连接MN.