题目内容
某大学毕业生参加一个公司的招聘考试,考试分笔试和面试两个环节,笔试有A、B两个题目,该学生答对A、B两题的概率分别为 和
和 ,两题全部答对方可过入面试,面试要回答甲、乙两个题目,该学生答对这两个题目的概率均为
,两题全部答对方可过入面试,面试要回答甲、乙两个题目,该学生答对这两个题目的概率均为 ,至少答对一题即可被聘用(假设每个环节的每个题目回答正确与否是相互独立的)
,至少答对一题即可被聘用(假设每个环节的每个题目回答正确与否是相互独立的)
(1)求该学生被公司聘用的概率;
(2)设该学生答对题目的个数为ξ,求ξ的分布列和数学期望.
解:(I)由题意记”答对A,B,甲,乙各题分别为事件A,B,C,D,
则P(A)= ,P(B)=
,P(B)= ,P(C)=P(D)=
,P(C)=P(D)= ,
,
由题意及事件之间为独立事件,故该学生被公司聘用的概率为:P(A•B)[1-P(C)P(D)]=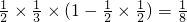 ,
,
(II)由题意由于随机变量ξ表示该学生答对题目的个数,由题意可得ξ的可能结果为:0,1,2,3,4,
并且P(ξ=0)=P( )=
)=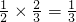 ,
,
P(ξ=1)=P(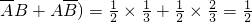 =
=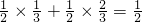 ,
,
P(ξ=2)=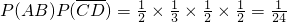 ,
,
P(ξ=3)=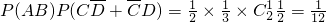 ,
,
P(ξ=4)=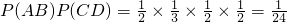 ,
,
所以随机变量ξ的分布列为:

所以随机变量的分布列为:Eξ=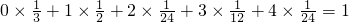
分析:(I)由题意记”答对A,B,甲,乙各题分别为事件A,B,C,D,由于事件之间为独立事件,故该学生被公司聘用的概率为:P(A•B)[1-P(C)P(D)],利用独立事件的公式即可算得;
(II)由题意由于随机变量ξ表示该学生答对题目的个数,由题意可得ξ的可能结果为:0,1,2,3,4,利用随机变量的定义及独立事件的概率公式借助于随机变量的定义求出每一个随机变量取值下对应的概率.在列出随机变量的分布列,并利用分布列求出其期望.
点评:此题主要考查了学生的理解题意的能力及计算能力与逻辑思维能力,还考查了独立事件同时发生的概率事件及随机变量的定义及其分布列,并考查了利用分布列求其期望.
则P(A)=
 ,P(B)=
,P(B)= ,P(C)=P(D)=
,P(C)=P(D)= ,
,由题意及事件之间为独立事件,故该学生被公司聘用的概率为:P(A•B)[1-P(C)P(D)]=
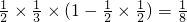 ,
,(II)由题意由于随机变量ξ表示该学生答对题目的个数,由题意可得ξ的可能结果为:0,1,2,3,4,
并且P(ξ=0)=P(
 )=
)=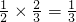 ,
,P(ξ=1)=P(
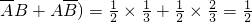 =
=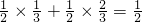 ,
,P(ξ=2)=
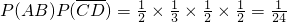 ,
,P(ξ=3)=
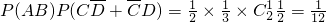 ,
,P(ξ=4)=
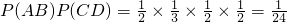 ,
,所以随机变量ξ的分布列为:

所以随机变量的分布列为:Eξ=
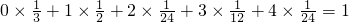
分析:(I)由题意记”答对A,B,甲,乙各题分别为事件A,B,C,D,由于事件之间为独立事件,故该学生被公司聘用的概率为:P(A•B)[1-P(C)P(D)],利用独立事件的公式即可算得;
(II)由题意由于随机变量ξ表示该学生答对题目的个数,由题意可得ξ的可能结果为:0,1,2,3,4,利用随机变量的定义及独立事件的概率公式借助于随机变量的定义求出每一个随机变量取值下对应的概率.在列出随机变量的分布列,并利用分布列求出其期望.
点评:此题主要考查了学生的理解题意的能力及计算能力与逻辑思维能力,还考查了独立事件同时发生的概率事件及随机变量的定义及其分布列,并考查了利用分布列求其期望.

练习册系列答案
相关题目
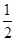 和
和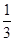 ,两题全部答对方可过入面试,面试要回答甲、乙两个题目,该学生答对这两个题目的概率均为
,两题全部答对方可过入面试,面试要回答甲、乙两个题目,该学生答对这两个题目的概率均为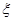 ,求
,求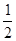 、
、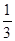 ,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为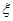 ,求
,求 、
、 ,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为
,两题全部答对方可进入面试.面试要回答甲、乙两个问题,该学生答对这两个问题的概率均为 ,求
,求