题目内容
对正整数n,设抛物线y2=2(2n+1)x,过P(2n,0)任作直线l交抛物线于An,Bn两点,则数列{
}的前n项和公式是______.
| ||||
| 2(n+1) |
设直线方程为x=ty+2n,代入抛物线方程得y2-2(2n+1)ty-4n(2n+1)=0,
设An(xn1,yn1),B(xn2,yn2),
则
•
=xn1xn2+yn1yn2=(t2+1)yn1yn2+2nt(yn1+yn2)+4n2,
用韦达定理代入得
•
=-4n(2n+1)(t2+1)+4n(2n+1)t2+4n2=-4n2-4n,
故
=-2n,
故数列{
}的前n项和-n(n+1),
故答案为-n(n+1).
设An(xn1,yn1),B(xn2,yn2),
则
| OAn |
| OBn |
用韦达定理代入得
| OAn |
| OBn |
故
| ||||
| 2(n+1) |
故数列{
| ||||
| 2(n+1) |
故答案为-n(n+1).

练习册系列答案
相关题目
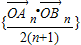 的前n项和公式是 .
的前n项和公式是 .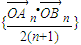 的前n项和公式是 .
的前n项和公式是 .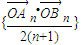 的前n项和公式是 .
的前n项和公式是 . 的前n项和公式是 .
的前n项和公式是 .